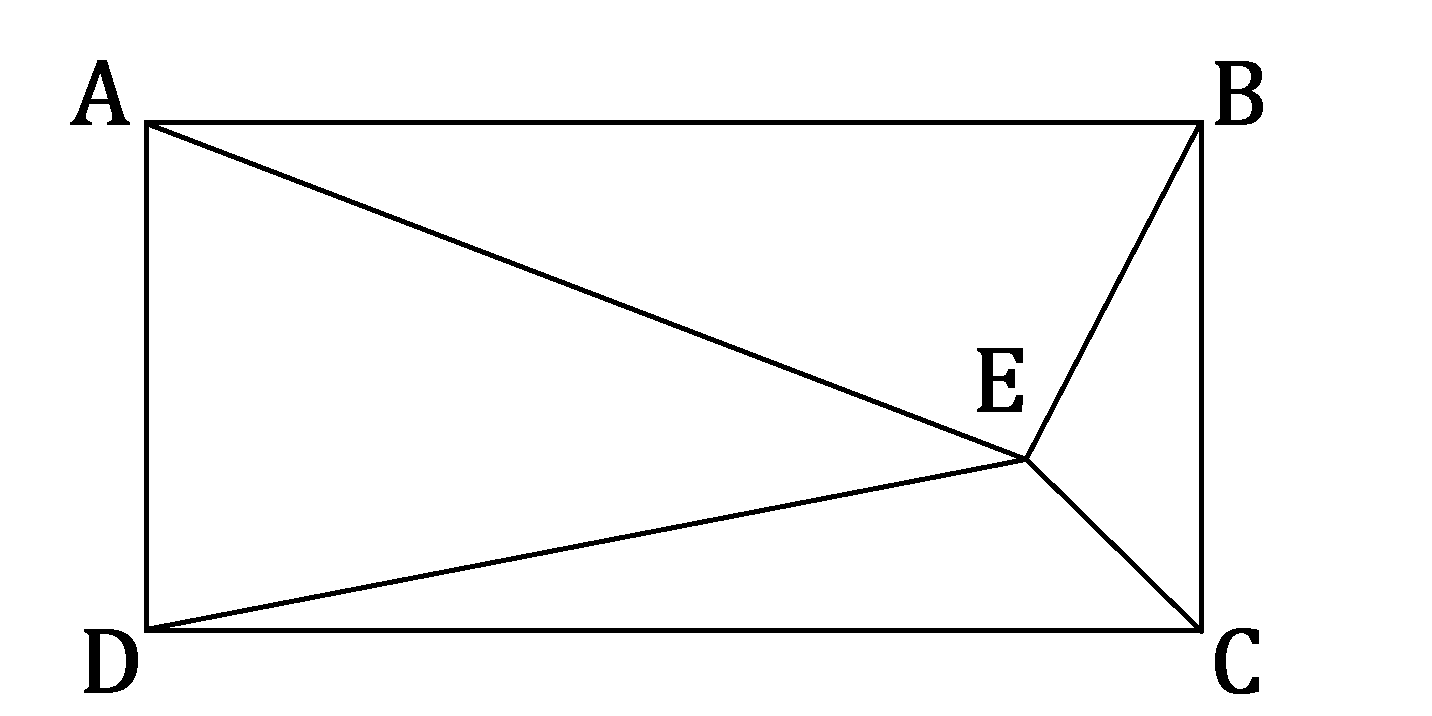
Mystery Spot

Relevant wiki: British Flag Theorem

According to the British Flag Theorem , if $E$ is a point within the rectangle $ABCD$ , then $AE^2 + CE^2 = BE^2 + DE^2$ .

Let $n = AE^2 + CE^2 = BE^2 + DE^2$ for some integer $n$ . We will then attempt to find the least possible natural number $n$ that can be written as the sum of two squares in two different ways.

Then for some integers $a$ and $b$ , $a^2 + b^2 = (a + bi)(a - bi)$ , which is the product of Gaussian integers or $|z|^2$ , and when plotting the Gaussian integers $z$ over the complex plane, we can draw a Gaussian circle of radius $|z|$ as the following examples:

The number of lattice points of $z$ on the circumference will then equal to the number of sums of squares for some natural number $n = |z|^2$ .

According to Sum of 2 Squares theorem, $n$ can be written as the sum of two squares if & only if $n$ only has prime factors $p = 4m + 1$ for some integer $m$ .

Now when expressing $n$ as prime factorization, $n = 2^{a_{0}}\cdot p_{1}^{a_{1}} \cdots p_{i}^{a_{i}} \cdot q_{1}^{b_{1}} \cdots q_{j}^{b_{j}}$ , where $p$ is a prime factor in a form of $4m + 3$ and $q$ is a prime factor in a form of $4m + 1$ .

If any $p$ has any odd number, the remainder will be $3$ in modulus $4$ , making the sum of squares impossible.

On the other hand, considering the powers of $q$ , the combination for each $q$ can be chosen from $0$ to $b_{j}$ . The overall combination $B = (b_{1} + 1)(b_{2} + 1)\cdots (b_{j} + 1)$ .

Considering only positive signs over the first quadrant in the complex plane, the number of sum of squares will then equal to $\dfrac{B}{2}$ as reflection over the line real part = imaginary part.

Altogether, the function for number of sums of squares, $r'_{2}(n)$ can be formulated as:

$r'_{2}(n) = \begin{cases} 0 & \quad \text{if} a_{i} \text{is odd} \\ \dfrac{B}{2} & \quad \text{if } a_{i} \text{is even and}B \text{ is even}\\ \dfrac{B - (-1)^{a_{0}}}{2} & \quad \text{if }a_{i} \text{is even and} B \text{ is odd}\\ \end{cases}$

Hence, our desired $r'_{n} = 2$ . For the second scenario, where $B$ is even, $B = 4$ . In this case, $B = (1+1)(1+1)$ or $B = 3+1$ . In other words, the number $n$ can be the product of two different primes or the cube of one prime.

For prime $q = 4m +1$ , the list involves: {5, 13, 17, ...}.

For lowest value possible, then $n = 5\cdot 13 = 65$ while $n = 5^3 =125$ , which is not the least number.

Now for the third scenario, where $B$ is odd, $B - (-1)^{a_{0}} = 4$ . Thus, $B = 3 = 2+1$ and $a_{0} = 1$ . Then $n = 2q^2$ , and the least value would be $n = 2\cdot 5^2 = 50$ .

Finally, from both scenarios, we can show that these numbers can really be written as two sums of two squares:

$50 = 1^2 + 7^2 = 5^2 + 5^2$

$65 = 1^2 + 8^2 = 4^2 + 7^2$

However, since the question specifically asks for different lengths within the rectangle, the only sum of the least possible four lengths = $1 + 8 + 4 + 7 = \boxed{20}$ .

It's simple to prove AE^2+CE^2=BE^2+DE^2

However the question is asked to find the distinct a,b,c,d such that a^2+b^2=c^2+d^2

One can use the well-known 15 for 15=4^2-1^2=8^2-7^2

Therefore 8^2+1^2=4^2+7^2 (by trial it is easy to prove that this is the minimum case)

Answer is 20