Mystery Triangle

Geometry Level 5

Triangle $X_1X_2X_3$ has $X_1X_2=1$ . Circles $\Gamma_1$ , $\Gamma_2$ , and $\Gamma_3$ are drawn such that $\Gamma_i$ has center $X_i$ and passes through $X_{i+1}$ ( $\Gamma_3$ passes through $X_1$ ).

Given that $\Gamma_1$ is internally tangent to $\Gamma_2$ at $P$ , and $\Gamma_3$ also passes through $P$ , then find the value of $(X_1X_2\cdot X_2X_3\cdot X_3X_1)^2$

The answer is 8.

2 solutions

Michael Mendrin
Sep 21, 2014

Consider points ${ X }_{ 2 },{ X }_{ 3 },P$ forming an isosceles of lengths ${ X }_{ 2 }{ X }_{ 3 }=P{ X }_{ 2 }=2$ and ${ X }_{ 3 }P=\sqrt { 2 }$ . And let $P{ X }_{ 1 }={ X }_{ 1 }{ X }_{ 2 }=1$ so that ${ X }_{ 3 }{ X }_{ 1 }=\sqrt { 2 }$ . Then all the conditions will be met, and we end up with ${ \left( 1\cdot \sqrt { 2 } \cdot 2 \right) }^{ 2 }=8$

Once you draw an accurate diagram, everything is relatively straightforward :)

Daniel Liu - 6 years, 8 months ago

Oh, you mean like this?

Mystery Triangle

Michael Mendrin - 6 years, 8 months ago

@Michael Mendrin Is it necessary that X1 lie on X2p??

Ash Dab - 6 years, 8 months ago

Ujjwal Rane
Oct 7, 2014

Imgur Imgur

In the diagram centers and circles are color matched

X1X2 = 1 . . . given

P, X1, X2 are co-linear . . . point of tangency and the two centers

X1X2 = X1P . . . . radii of green circle

X2P = 2 (X2X1) = 2 = X2X3 . . . . radii of red circle

Finally, X3X1 = X3P = b say . . . radii of blue circle

Triangles PX2X3 and X1X3P are both isosceles and have a common base angle P hence are similar too.

Thus, 2/b = b/1. That is b = sqrt(2)

Thus (X1X2.X2X3.X3X1)^2 = 8

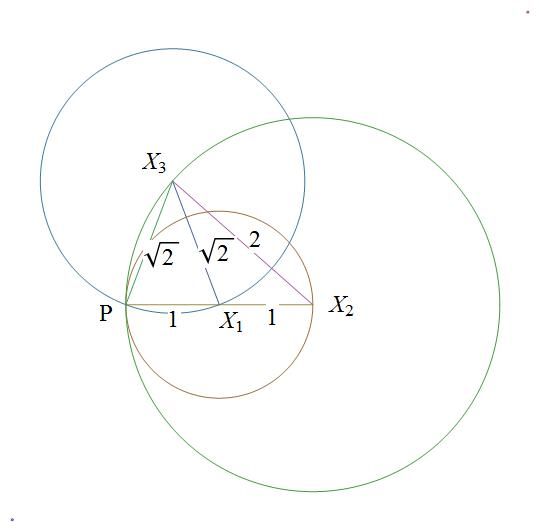
Mystery Triangle

The answer is 8.

2 solutions

0 pending reports