Mystic Darkness
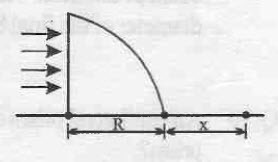 A uniform, horizontal beam of light is incident upon a quarter cylinder of radius
, and has a refractive index
. Starting at a distance
from the front of the cylinder, the table is not illuminated.
A uniform, horizontal beam of light is incident upon a quarter cylinder of radius
, and has a refractive index
. Starting at a distance
from the front of the cylinder, the table is not illuminated.
Find the value of (in cm ).
Details and Assumptions:
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a point P on the curved surface at an angle θ to the horizontal. Since at the first interface the light undergoes normal incidence, it will suffer no deviation. As a result the light will strike the curved surface horizontally and hence at P also. Using simple geometry, we can observe and obtain that such a ray will strike at an angle θ to the normal at P . Using Snell's law, we obtain the equation μ g l a s s s i n ( θ ) = μ a i r s i n ( r ) , where r is the angle of refraction in air. Clearly, as θ increases, r will also increase. Also, the distance from the center of the cylinder (and indirectly from where distance x is measured) where the ray strikes after refraction strikes the surface (on which the cylinder rests) decreases as θ increases.
As θ goes on increasing, we would obtain a value such that r = 9 0 ∘ , i.e., critical angle for the given pair of optical media. For points having θ greater than this value, the light rays would suffer Total Internal Reflection and hence will not come outside the cylinder. Hence, we would obtain a dark patch.
At r = 9 0 ∘ , θ = i c ⇒ μ g l a s s sin ( i c ) = 1 . sin ( 9 0 ∘ ) .
3 2 sin ( i c ) = 1 ⇒ sin ( i c ) = 2 3
⇒ i c = 6 0 ∘
Clearly, at the point where this specific refracted ray will strike the ground will be the point to the left of which the dark region would exist. By elementary geometry, we get,
R + x = R sec ( i c ) ⇒ x = R sec ( 6 0 ∘ ) − R = 2 R − R = R
x = 5 c m