N cube build x layers
N
pics small wooden blocks (all of the same size cube). Quickly build the shape of the rule as shown in the following figure (the figure below is the scale of 5 levels), and request the maximum number of layers.
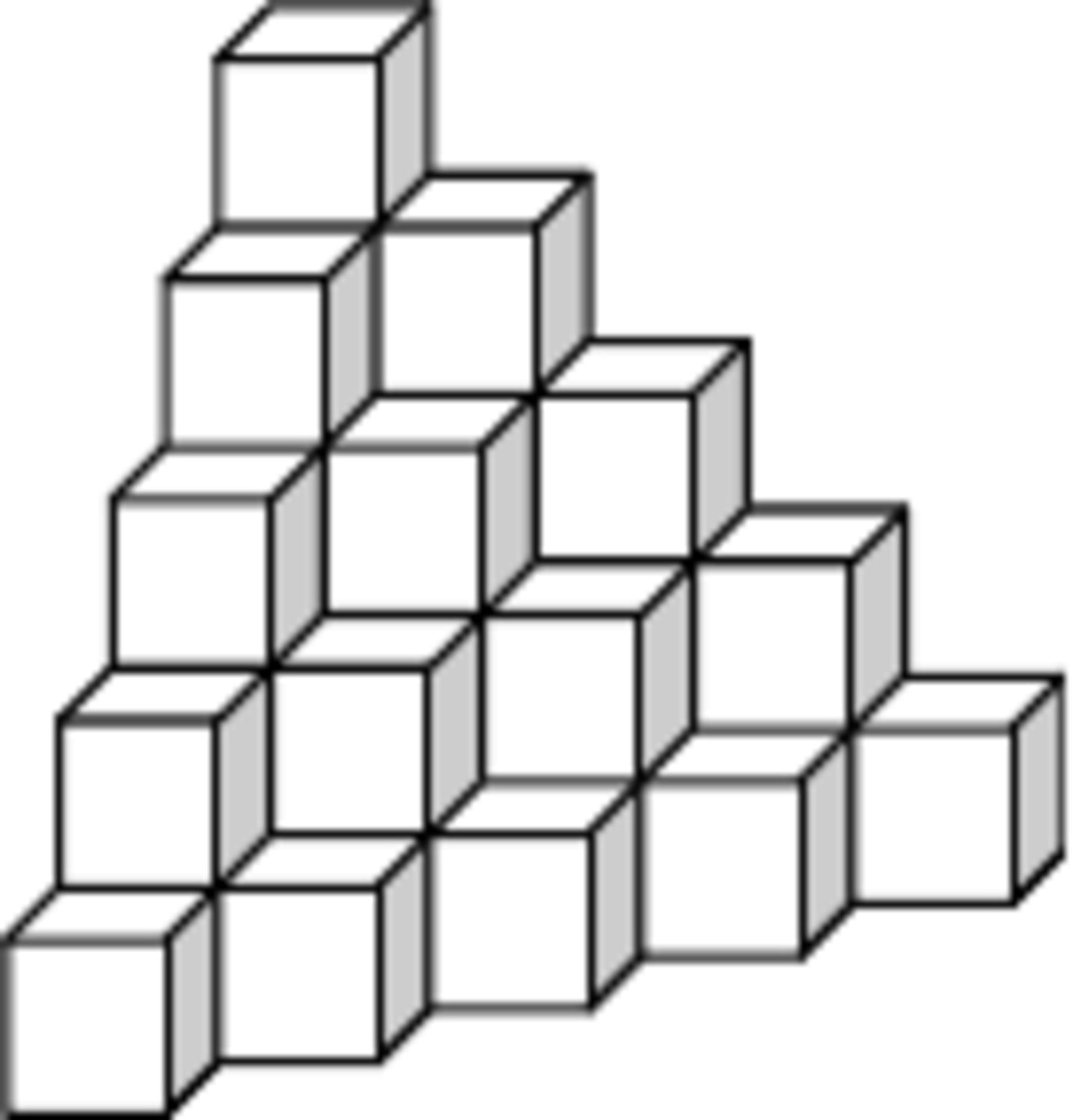
If you have integer 1000 pics small blocks, What is the max number of layers that can be stacked = x, and the number of remaining wooden block = y? you can input result suit to the format as follow: if x equal to 10 and y equal to 23 , then you prefer to input 10.23
The answer is 17.31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume the sequence { a n } n = 1 ∞ to be the number of cubes in each level. then, the following recurrence relation is true.
a n = a n − 1 + n + 1
the corresponding generating function is
f ( x ) = ( 1 − x ) 3 1
the generating function that has b m = ∑ i = 0 m a i as its coefficient is (we are adding the number of cubes for m levels)
g ( x ) = 1 − x f ( x ) = ( 1 − x ) 4 1
if the Taylor expansion of g ( x ) , around 0 , is written, one finds out that the coefficients of g ( x ) are b m = m ! 3 ! ( 3 + m ) ! = ( 3 m + 3 ) . Then we need to find the maximum m for which
b m = ( 3 m + 3 ) ≤ 1 0 0 0
it turns out to be m = 1 6 , which means that we can have 17 levels. Also, ( 3 1 6 + 3 ) = ( 3 1 9 ) = 9 6 9 , so the remaining of the cubes can be calculated.