A Huge Sum of Interior Angles
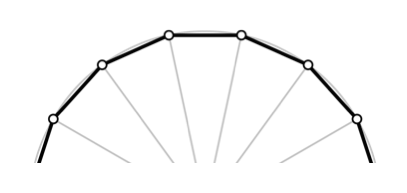
The sum of the measures of the interior angles of an -gon is . How many sides does this -gon have?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To solve this problem, you need to know the following formula:
Sum of the angles in an n -gon = ( n − 2 ) × 1 8 0 ∘ .
n is the number of sides. So just plug in the numbers and solve
2 3 4 0 ∘ 2 3 4 0 ∘ 2 3 4 0 ∘ + 3 6 0 ∘ 2 7 0 0 ° 1 8 0 ∘ 2 7 0 0 ∘ 1 5 = ( n − 2 ) × 1 8 0 ∘ = 1 8 0 ∘ n − 3 6 0 ∘ = 1 8 0 ∘ n − 3 6 0 ° + 3 6 0 ∘ = 1 8 0 ∘ n = 1 8 0 ∘ 1 8 0 ∘ n (Dividing both sides by 1 8 0 ∘ ) = n
Therefore,the n -gon has 1 5 sides