Nagel Angle Ankle II
Let denote the set of all triangles, such that:
- One of the three points (green) on the circumference of the circumcircle is fixed;
- The inradius is , and the circumradius is .
An example of one such triangle is illustrated as shown below:
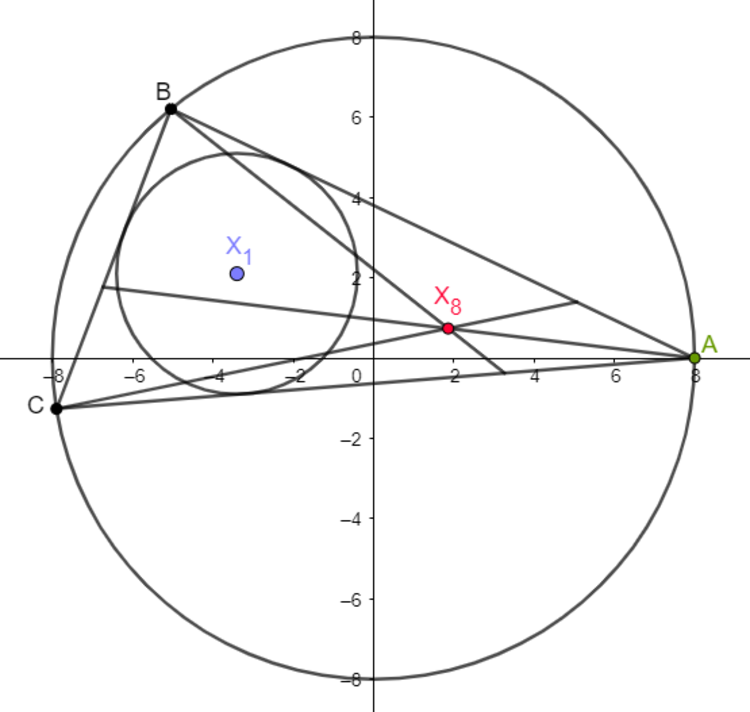
Find the locus of the Nagel point of all such triangles. If its arc length (not repeated) can be expressed as , where is a positive real-valued constant, input as your answer.
Bonus. What if suppose we solve this problem, but for the fixed incenter ?
The answer is 4.0000000000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Standard results give the distances between the outcentre O of a triangle and its incentre I and Nagel point N a as: O I = R ( R − 2 r ) O N a = a b c 4 Δ O I 2 = a b c 4 R Δ ( R − 2 r ) where R , r are the outradius and inradius, and Δ is the area. Since R = 4 Δ a b c we deduce that O N a = R − 2 r In this case we deduce that O N a = 8 − 2 × 3 = 2 .
For a fixed vertex A and given vertex B on a circle of radius 8 , there are two possible triangles A B C with inradius 3 and outradius 8 , one being the mirror image of the other in the perpendicular bisector of A B . Thus there are two candidates for the Nagel point, and they are mirror images of the other in the same line. As B varies, the two candidate Nagel points provide a double cover of the circle with centre O and radius 2 , which has perimeter 4 π , making the answer 4 .
Clearly we have O I = 4 in this case, so the locus of the incentre is a circle of radius 4 , centre O , and hence has perimeter 8 π .