Nagel Angle Ankle
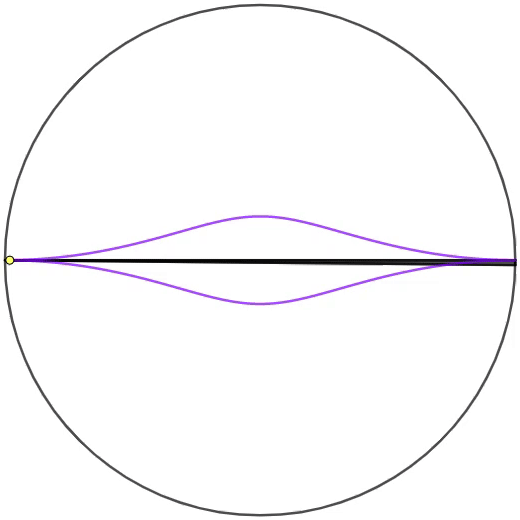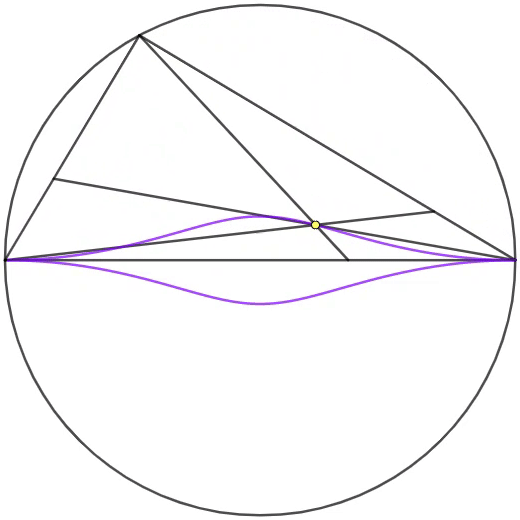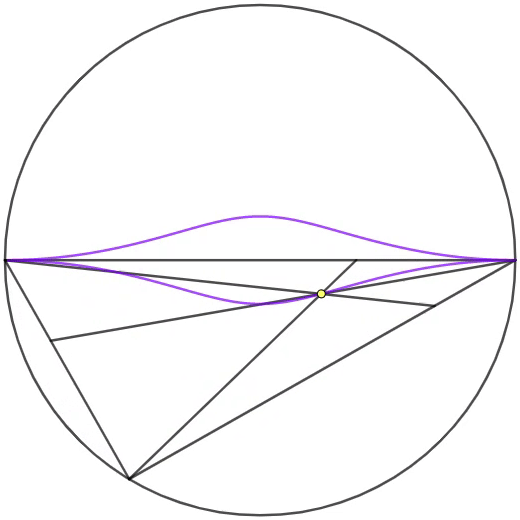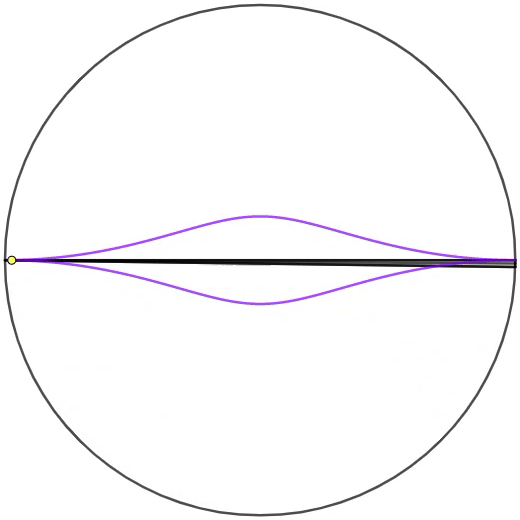
The animation on the right shows the circle inscribing the triangle whose one of the sides is the diameter with two fixed endpoints. The point is selected and rotated counterclockwise on the circumference, so that the Nagel point of the triangle forms the locus colored in purple.
If the following area ratio is
R = area of the whole circle area bounded inside the locus
Input ⌊ 1 0 6 R ⌋ as your answer.
The answer is 92958.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
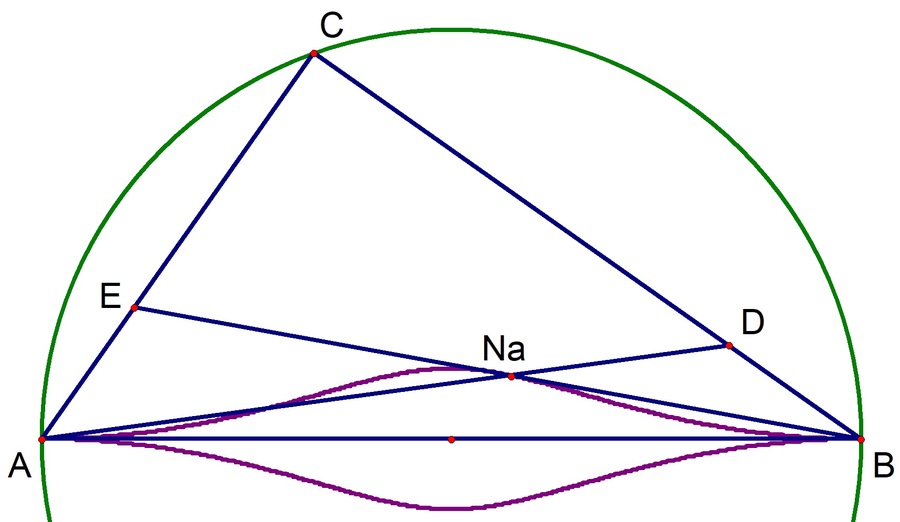 If the points
A
,
B
,
C
have coordinates
(
−
1
,
0
)
,
(
1
,
0
)
and
(
cos
2
θ
,
sin
2
θ
)
respectively (we are writing
∠
B
A
C
=
θ
), then the Nagel points
N
a
is the intersection of the lines
A
D
and
B
E
, where
2
+
A
E
=
2
+
B
D
is equal to the semiperimeter
1
+
cos
θ
+
sin
θ
of the triangle
A
B
C
. This means that
D
E
(
1
−
(
sin
θ
+
cos
θ
−
1
)
sin
θ
,
(
sin
θ
+
cos
θ
−
1
)
cos
θ
)
(
−
1
+
(
sin
θ
+
cos
θ
−
1
)
cos
θ
,
(
sin
θ
+
cos
θ
−
1
)
sin
θ
)
and hence the Nagel point has coordinates
N
a
(
x
(
θ
)
,
y
(
θ
)
)
=
(
cos
2
θ
+
2
sin
θ
−
2
cos
θ
,
(
sin
θ
+
cos
θ
−
1
)
2
)
and so the upper half of the area enclosed by the locus of the Nagel point is
A
=
∫
0
2
1
π
x
′
(
θ
)
y
(
θ
)
d
θ
=
8
−
2
5
π
Thus the desired proportion is
R
=
π
2
A
=
π
1
6
−
5
=
0
.
0
9
2
9
5
8
1
7
8
9
4
.
.
.
and hence
⌊
1
0
6
R
⌋
=
9
2
9
5
8
.
If the points
A
,
B
,
C
have coordinates
(
−
1
,
0
)
,
(
1
,
0
)
and
(
cos
2
θ
,
sin
2
θ
)
respectively (we are writing
∠
B
A
C
=
θ
), then the Nagel points
N
a
is the intersection of the lines
A
D
and
B
E
, where
2
+
A
E
=
2
+
B
D
is equal to the semiperimeter
1
+
cos
θ
+
sin
θ
of the triangle
A
B
C
. This means that
D
E
(
1
−
(
sin
θ
+
cos
θ
−
1
)
sin
θ
,
(
sin
θ
+
cos
θ
−
1
)
cos
θ
)
(
−
1
+
(
sin
θ
+
cos
θ
−
1
)
cos
θ
,
(
sin
θ
+
cos
θ
−
1
)
sin
θ
)
and hence the Nagel point has coordinates
N
a
(
x
(
θ
)
,
y
(
θ
)
)
=
(
cos
2
θ
+
2
sin
θ
−
2
cos
θ
,
(
sin
θ
+
cos
θ
−
1
)
2
)
and so the upper half of the area enclosed by the locus of the Nagel point is
A
=
∫
0
2
1
π
x
′
(
θ
)
y
(
θ
)
d
θ
=
8
−
2
5
π
Thus the desired proportion is
R
=
π
2
A
=
π
1
6
−
5
=
0
.
0
9
2
9
5
8
1
7
8
9
4
.
.
.
and hence
⌊
1
0
6
R
⌋
=
9
2
9
5
8
.
@Mark Hennings , we really liked your comment, and have converted it into a solution.
@Mark Hennings , first of all, as always, great solution, sir! My approach was exactly the same as yours (I wonder if someone tried to determine y ( x ) explicitly).
I have a question to you: How did you find the coordinates of the Nagel point, having found the coordinates of D and E ? I went all the way through of finding the equations of the lines A D and B E and then solving the resulting system (as N a = A D ∩ B E ). The trigonometric expression were a huge mess so I mistook somewhere in the process and got a wrong result.
So...did you do it any smarter than me or you were much more accurate transforming these nasty expressions?