Do me a solid

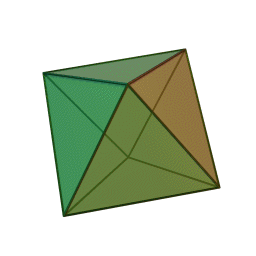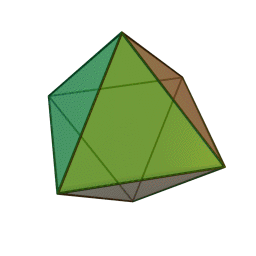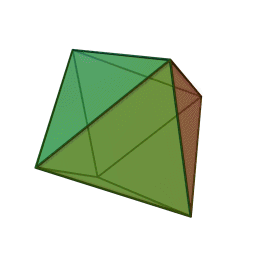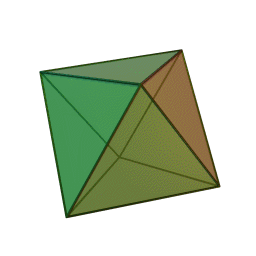
$|x|+|y|+|z|\Rightarrow$ the shape will be symmetric w.r.t. all $8$ octant. So if we could find the part of it in one octant, we'll be able to easily deduce whole shape.
The most easy part to consider is that in $1^{\text{st}}$ octant, which is $x+y+z=3$ which is plane passing through $\left(1,1,1\right)$ and perpendicular to vector $\hat{i}+\hat{j}+\hat{k}$ . This when reflected in other octant gives shape of octahedron.

The solid consists of eight equilateral triangles with vertices joined at $(0,0,\pm3), (0,\pm3,0)$ , and $(\pm3,0,0)$ ,

which describes an $\boxed{octahedron}$