NAND Blocks

Computer Science Level 2

N A N D NAND and N O R NOR gates are said to be the building block gates of all digital logic circuits because all other logic gates can be implemented using only the combinations of multiple N A N D NAND or N O R NOR gates.

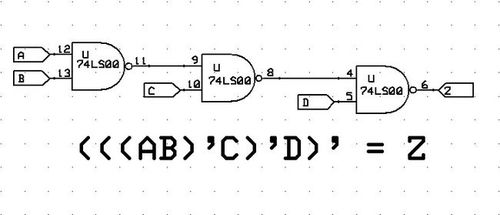
What is the minimum number of N A N D NAND gates needed to implement X O R XOR logic?

This problem is not original.
Learn more about logic gates .
5 2 6 7 4

View wiki
Daniel Cabrales by Daniel Cabrales , 24, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Michael Mendrin
Jun 8, 2015

The algebraic versions of the logic gates in question are, for inputs p , q p, q

N A N D ⟷ 1 − p q NAND \longleftrightarrow 1-pq
X O R ⟷ p + q − 2 p q XOR \longleftrightarrow p+q-2pq

Let r = 1 − p q r = 1-pq , which is the output of the first N A N D NAND gate. Then

p ′ = 1 − r p p'=1-rp
q ′ = 1 − r q q'=1-rq

are the outputs of two more N A N D NAND gates. From these, we use 1 1 more N A N D NAND gate with the output

1 − p ′ q ′ 1-p'q'

When expanded, this works out to

p + q − p q − p 2 q − p q 2 + 2 p 2 q 2 − p 3 q 3 p+q-pq-{ p }^{ 2 }q-p{ q }^{ 2 }+2{ p }^{ 2 }{ q }^{ 2 }-{ p }^{ 3 }{ q }^{ 3 }

which, after eliminating the exponents (making them all 1 1 ), reduces to

p + q − 2 p q p+q-2pq

which is the algebraic version of the X O R XOR gate. Hence 4 4 N A N D NAND gates are used. The solution leads from the fact the terms p p and q q must be introduced in order to emulate an X O R XOR gate.

Note: These algebraic equivalents are based on T r u e ⟷ 1 True \longleftrightarrow 1 and F a l s e ⟷ 0 False \longleftrightarrow 0

Note also: This approach isn't orthodox.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

The written formula with N A N D NAND s does contain 5 occurrences of N A N D NAND . However, a silly mistake on my part, not realizing that I did not need to calculate r r twice.

Stephen Tosh - 6 years ago

Log in to reply

We did this in our electronics practicals .

Rushikesh Joshi - 6 years ago

I answered 5, because i didn't noticed i had a shared term in the final result. a X O R b = a . b ‾ + a ‾ . b = a . a ‾ + a . b ‾ + a ‾ . b + b . b ‾ = a ( a ‾ + b ‾ ) + b ( a ‾ + b ‾ ) = a ( a ‾ + b ‾ ) + b ( a ‾ + b ‾ ) ‾ ‾ = a ( a ‾ + b ‾ ) ‾ . b ( a ‾ + b ‾ ) ‾ ‾ = a ( a ‾ + b ‾ ‾ ‾ ) ‾ . b ( a ‾ + b ‾ ‾ ‾ ) ‾ ‾ = a ( a . b ‾ ) ‾ . b ( a . b ‾ ) ‾ ‾ = a N A N D ( a N A N D b ) ) N A N D ( b N A N D ( a N A N D b ) ) \begin{aligned} a\,XOR\,b &= a.\overline{b}+\overline{a}.b\\ &= a.\overline{a}+a.\overline{b}+\overline{a}.b+b.\overline{b}\\ &= a(\overline{a}+\overline{b})+b(\overline{a}+\overline{b})\\ &= \overline{\overline{a(\overline{a}+\overline{b})+b(\overline{a}+\overline{b})}}\\ &= \overline{\overline{a(\overline{a}+\overline{b})}.\overline{b(\overline{a}+\overline{b})}}\\ &= \overline{\overline{a(\overline{\overline{\overline{a}+\overline{b}}})}.\overline{b(\overline{\overline{\overline{a}+\overline{b}}})}}\\ &= \overline{\overline{a(\overline{a.b})}.\overline{b(\overline{a.b})}}\\ &= a\,NAND\,(a\,NAND\,b))\,NAND\,(b\,NAND\,(a\,NAND\,b)) \end{aligned}

Jose Solsona - 5 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...