Napkin Rings (Including Some Big Ones)
 Credit: Wikipedia
Credit: Wikipedia
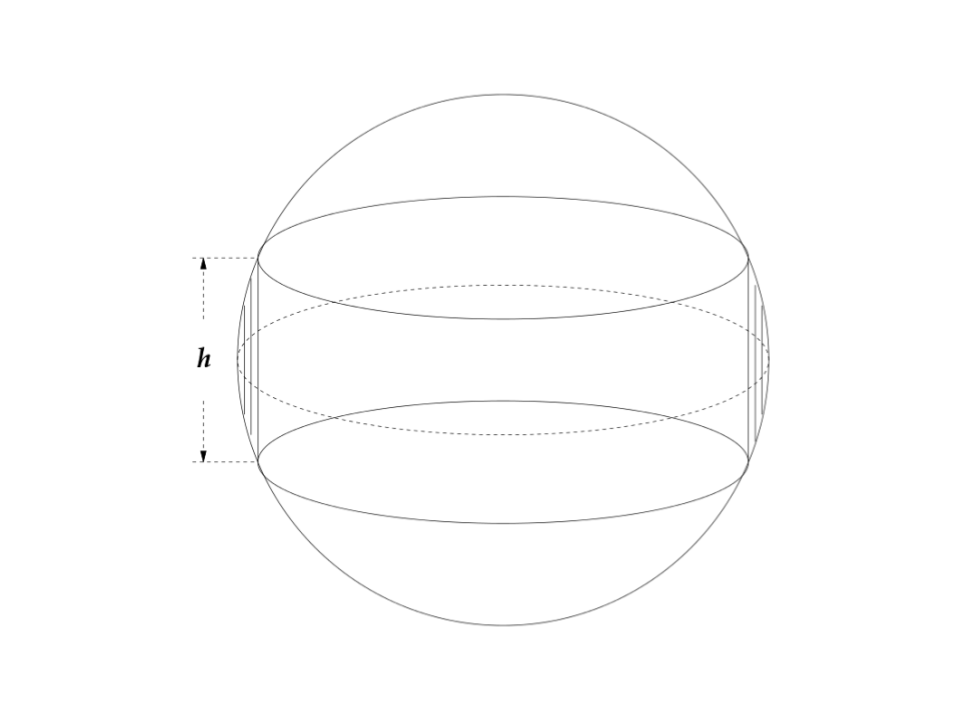
Take a sphere, and pass a cylinder through it, such that its central axis intersects the sphere's centre. Call the height of the cylindrical portion inscribed within the sphere . The torus-like band with height delimited by the cylindrical portion is called a napkin ring .
Suppose we took the Earth and an orange, and identified napkin rings of identical height for both. What is the difference in volume between both?
Assume that the Earth and the orange are both perfect spheres, and that the initial cylinder's height is infinite.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is given by the setting of the puzzle that there is a single well-defined numerical answer in R (real numbers). As the radii of the spheres in question are not given, the answer must be independent of the radii. As the answer is the difference between two volumes, each volume must be independent of the corresponding radius (proof left as an exercise to the reader). Therefore, the volumes are identical and their difference is zero.