Napoleon’s Triangle
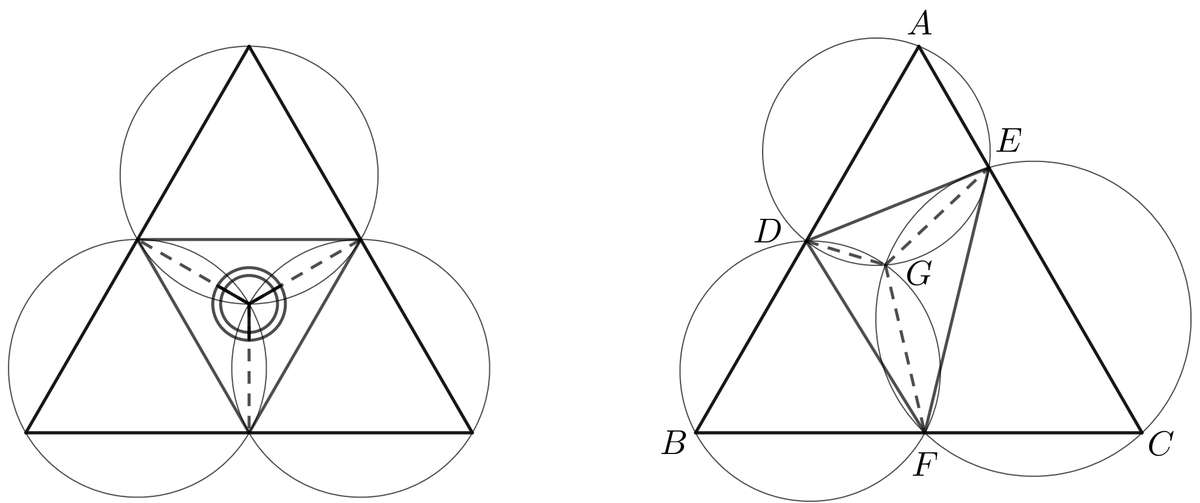
In the equilateral triangle A B C , points D , E and F are positioned on their respective edges, such that:
- Each of the three circles pass through 3 points - 1 vertex and the remaining each on the distinct edge.
- Their intersection point G lies inside the equilateral triangle, but not on its boundary.
As shown on the left, it is possible for m ∠ D G F = m ∠ F G E = m ∠ E G D = 1 2 0 ∘ for D , E and F being midpoints. Does that hold for any other point arrangement?
Bonus: Determine the probability of the point arrangement, satisfying those given conditions (if multiple arrangements exist).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice argument. But proving that infinitely many arrangements exist that have the angles 120° is not the same as proving that none exist with different angles. Could you prove it for any arbitrary choice of D,E,F?
If A D = B F = C E , then m ∠ D G F = m ∠ F G E = m ∠ E G D = 1 2 0 ° .
Proof: Let T be the center of the equilateral triangle, and let O be the center of the circle passing through E , G , F , and C . Also let A D = B F = C E .
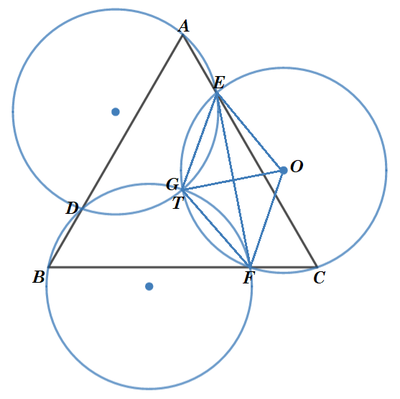
By symmetry, ∠ C F T = ∠ A E G . By the properties of a straight line, ∠ C E T = 1 8 0 ° − ∠ A E G = 1 8 0 ° − ∠ C F T . By the angle sum property of quadrilateral C F T E , ∠ F T E + ∠ C E T + ∠ E C F + ∠ C F T = 3 6 0 ° , or ∠ F T E + ( 1 8 0 ° − ∠ C F T ) + 6 0 ° + ∠ C F T = 3 6 0 ° , which solves to ∠ F T E = 1 2 0 ° .
Also by symmetry, T E = T F . That means △ F T E is an isosceles triangle, and since ∠ F T E = 1 2 0 ° , its base angles are ∠ T E F = ∠ T F E = 3 0 ° .
Since central ∠ E O F subtends the same arc as inscribed ∠ E C F , ∠ E O F = 2 ⋅ ∠ E C F = 2 ⋅ 6 0 ° = 1 2 0 ° . Since △ E O F is an isosceles triangle, and since ∠ E O F = 1 2 0 ° , its base angles are ∠ O E F = ∠ O F E = 3 0 ° .
Then △ F T E ≅ △ E O F by ASA congruence, which means T E = T F = O E = O F . Since T E = O E and ∠ T E O = ∠ T E F + ∠ O E F = 3 0 ° + 3 0 ° = 6 0 ° , △ O T E is an equilateral triangle, and O T = O E = O F . Therefore, T is on circle O .
By similar arguments, T is on the other two circles as well. Therefore, G and T are the same point such that m ∠ D G F = m ∠ F G E = m ∠ E G D = 1 2 0 ° .
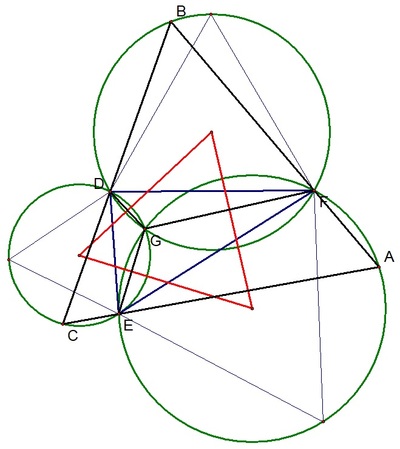 Napoleon's Theorem (
le petit empereur
had no part in working this out) states that if you construct equilateral triangles on the sides of any triangle
D
E
F
, the centres of these triangles form an equilateral triangle (in red). If we construct the circumcircles of these triangles, then they all meet at the point
G
, where
∠
D
G
E
=
∠
E
G
F
=
∠
F
G
D
=
1
2
0
∘
. The point
G
is called the first Fermat point of
D
E
F
. Since (for example)
∠
E
A
F
=
6
0
∘
for any point
A
on the major arc
E
F
, we can choose any point
A
on this arc, and draw straight lines from
A
through
E
and
F
to intersect the other circumcircles at
C
and
B
respectively. Then
A
B
C
is an equilateral triangle with the desired properties. This works provided that all of the angles in
D
E
F
are less than
1
2
0
∘
, which means that
G
lies inside the triangle
D
E
F
.
Napoleon's Theorem (
le petit empereur
had no part in working this out) states that if you construct equilateral triangles on the sides of any triangle
D
E
F
, the centres of these triangles form an equilateral triangle (in red). If we construct the circumcircles of these triangles, then they all meet at the point
G
, where
∠
D
G
E
=
∠
E
G
F
=
∠
F
G
D
=
1
2
0
∘
. The point
G
is called the first Fermat point of
D
E
F
. Since (for example)
∠
E
A
F
=
6
0
∘
for any point
A
on the major arc
E
F
, we can choose any point
A
on this arc, and draw straight lines from
A
through
E
and
F
to intersect the other circumcircles at
C
and
B
respectively. Then
A
B
C
is an equilateral triangle with the desired properties. This works provided that all of the angles in
D
E
F
are less than
1
2
0
∘
, which means that
G
lies inside the triangle
D
E
F
.
If we assume that one arrangement is possible as shown in the left figure, then it is possible for infinitely many arrangement. This can be proved as shown below :
Taking the left figure and name various points as shown in right figure. If we rotate those dotted lines about intersection point G then we get another arrangement of points D , E , F . Also ∠ D G F = ∠ F G E = ∠ E G D = 1 2 0 ° . Since ∠ D G F = 1 2 0 ° and ∠ D B F = 6 0 ° we get that quadrilateral D B F G is cyclic. Similarly other 2 quadrilaterals namely C F G E and A D G E are also cyclic. All these three quadrilateral have only 1 vertex in common namely G . Hence all three circles will intersect at single point G . Also if we move the intersection point G then we get different intersection point of circles.
In other words, if we take any point G inside the triangle and make three lines G D , G E , G F in the plane of triangle such that ∠ D G F = ∠ F G E = ∠ E G D = 1 2 0 ° to intersect the sides at D , E , F then construction of such circles will always be possible. Hence taking different point G and different orientation of lines G D , G E , G F we get different points D , E , F .