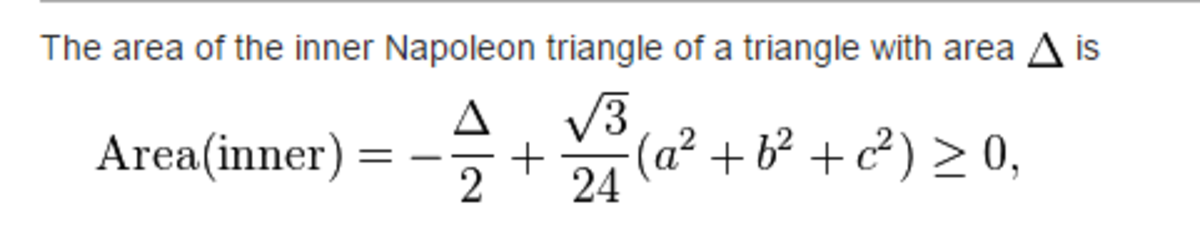Napoleon's?
Define triangle A B C with A B = 5 5 units, B C = 6 0 units and A C = 4 9 units. Let D , E and F be points outside the triangle such that triangles A B D , B C E and A C F are equilateral. Points G , H and I are the centroids of the three equilateral triangles, respectively. Find the area of triangle G H I .
Submit your answers up to three decimal places.
The answer is 1285.305.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I have made my own formula in finding the sides of the triangle formed by those centroids.. Let a , b and c be the sides of the triangle A B C , d be the side of triangle G H I , we have 3 d 2 = 2 s 2 + ( 1 2 ( s ) ( s − a ) ( s − b ) ( s − c ) ) 0 . 5 − ( a b + b c + a c ) .
Let O be the circumcenter of triangle ABC and G, H, I those of equilateral triangles.
X, Y, Z are midpoint of BC, CA, AB respectively. R the circumradius of triangle ABC.
I
n
Δ
A
B
C
,
S
i
n
A
=
S
i
n
{
C
o
s
−
1
(
2
∗
A
B
∗
A
C
A
B
2
+
A
C
2
−
B
C
2
)
}
=
S
i
n
{
C
o
s
−
1
(
2
∗
4
9
∗
5
5
4
9
2
+
5
5
2
−
6
0
2
)
}
=
0
.
9
4
0
8
7
S
i
n
B
=
A
C
∗
B
C
S
i
n
A
=
0
.
8
6
2
4
6
a
n
d
S
i
n
C
=
0
.
7
6
8
3
7
I
n
q
u
a
d
r
i
l
a
t
e
r
a
l
A
Z
O
Y
,
∠
A
Z
O
=
∠
O
Y
A
=
9
0
o
.
∴
S
i
n
G
O
I
=
S
i
n
A
,
S
i
m
i
l
a
r
l
y
S
i
n
H
O
G
=
S
i
n
B
S
i
n
I
O
H
=
S
i
n
C
.
R
=
2
∗
S
i
n
A
B
C
=
3
1
.
8
8
5
0
.
G
Z
a
n
d
Z
O
a
r
e
⊥
A
B
a
t
Z
,
∴
G
O
i
s
a
s
t
.
l
i
n
e
.
∴
G
O
=
G
Z
+
Z
O
=
r
3
+
r
c
=
R
2
−
(
2
A
B
)
2
+
2
A
B
∗
T
a
n
3
0
.
G
O
=
3
1
.
8
8
5
0
2
−
(
2
4
9
)
2
+
2
4
9
∗
3
1
=
3
4
.
5
5
1
8
.
S
i
m
i
l
a
r
l
y
I
O
=
3
2
.
0
5
1
H
O
=
2
8
.
1
2
2
5
.
A
r
e
a
Δ
G
O
I
=
2
1
∗
G
O
∗
I
O
∗
S
i
n
A
=
2
1
∗
3
4
.
5
5
1
8
∗
3
2
.
0
5
1
∗
0
.
9
4
0
8
7
.
A
r
e
a
Δ
G
H
I
=
A
r
e
a
Δ
G
O
I
+
A
r
e
a
Δ
H
O
G
+
A
r
e
a
Δ
I
O
H
.
=
2
1
∗
3
4
.
5
5
1
8
∗
3
2
.
0
5
1
∗
0
.
9
4
0
8
7
+
2
1
∗
3
2
.
0
5
1
∗
2
8
.
1
2
2
5
.
∗
0
.
7
6
8
3
7
+
2
1
∗
2
8
.
1
2
2
5
.
∗
3
4
.
5
5
1
8
∗
0
.
8
6
2
4
6
.
A
r
e
a
Δ
G
H
I
=
1
2
8
5
.
3
0
4
7
THIS PROBLEM CAN ALSO BE SOLVED AS UNDER.
After finding out angles A, B, and C, in degrees, adding 60 to them give us
∠
s
I
A
G
,
G
B
H
,
H
C
I
.
I
A
=
I
C
=
3
5
5
,
G
B
=
G
A
=
3
4
9
,
H
C
=
H
B
=
3
6
0
Apply Cos Rule to find the three sides.
Knowing the three sides the area can be found by Hero’ Formula.
Nice solution Mark! I've discovered a shorter formula as well!