Nash Equilibrium

Logic Level 1

How many Nash equilibria does the following game have? Assume that we restrict ourselves to pure strategies (that is, each agent can only pick exactly one strategy).


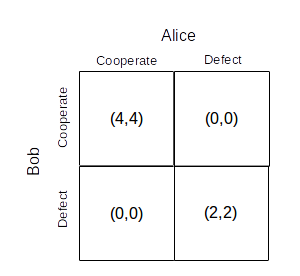
The answer is 2.

View wiki
Adam Strandberg by Adam Strandberg , 28, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Eli Ross Staff
Apr 5, 2016

Both C/C and D/D are pure strategy Nash equilibriums, since changing one's behavior (while the other person stays the same) would mean giving up something (4 or 2) to get nothing (0).

19 Helpful 2 Interesting 0 Brilliant 9 Confused

Why? What about "both will fear that other may Defect .. so they wiill chose logically min loss situation and both settles for D/D"

C/C is ni fear situation .. not very realistic. It has the same possibility to be chosen over D/D as that of C/D or D/C.

Ananya Aaniya - 4 years, 7 months ago

I thought C/C was the only Nash equilibrium. C/C offers the highest payoff for both players. When one person is deciding between C and D, they will see that both they and the other player has a higher payoff by both choosing C so they should know it’s better to choose C. So why would they choose D/D?

J Amin - 6 months ago
Leaf H
Apr 6, 2021

If u defect it's either 2 years or 0 but if u C it's either 0 or 4 So i think d/d is most possible But the thing is that if you know this is how the other person reacts u might decide to choose C because that might get you a better result. Tho there's a chance the other one thinks the same way and you get the worst result you want to completely unable the worst result to happen. so I really don't know if it's 1 or 2

0 Helpful 1 Interesting 0 Brilliant 0 Confused

This scenario is assuming the numbers are mutually acceptable objects, and not years of something no one wants.

Aaren Ruparel - 4 weeks, 1 day ago
Aaren Ruparel
May 17, 2021

Both C/C and D/D are Nash equilibriums since changing to get a different behavior than the other one, neither will get anything. Assuming they can determine what they want to do with the other player beforehand, C/C and D/D are Nash equilibriums. If they cannot determine what they want with the other player, the most likely scenario is D/D.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...