Nasty bounding

Calculus Level 4

t ( x ) = 1 x 2 − a 2 h ( x ) = 1 a 2 − x 2 b ( x ) = 1 x 2 + a 2 \begin{aligned} \large t(x)&=&\frac{1}{\sqrt{x^{2}-a^{2}}} \\ \large h(x)&=&\frac{1}{\sqrt{a^{2}-x^{2}}} \\ \large b(x)&=&\frac{1}{\sqrt{x^{2}+a^{2}}} \end{aligned}

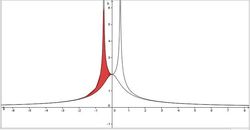
Let there be three functions: the trunk, the hamper and the bell as described above.

In pairs, they are to one another asymptotically, except for the bell and the hamper, which effectively meet each other.

Find the red area when a = 0.5 a=0.5 .

Details and assumptions :

  • The drawing was an attempt to indicate that they "touch" each other. I'm not good at this, though.

  • Can you find a general formula for the area as a function of a a ?


The answer is 1.57.

View wiki
Mikael Marcondes by Mikael Marcondes , 24, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

James Wilson
Jan 15, 2021

Area = ∫ − ∞ − a [ 1 x 2 − a 2 − 1 x 2 + a 2 ] d x + ∫ − a 0 [ 1 a 2 − x 2 − 1 x 2 + a 2 ] d x \int_{-\infty}^{-a} \Big[\frac{1}{\sqrt{x^2-a^2}}-\frac{1}{\sqrt{x^2+a^2}}\Big]dx+\int_{-a}^0 \Big[\frac{1}{\sqrt{a^2-x^2}}-\frac{1}{\sqrt{x^2+a^2}}\Big]dx

= [ ln ⁡ ∣ x a + x 2 a 2 − 1 ∣ − ln ⁡ ∣ x a + x 2 a 2 + 1 ∣ ] − ∞ − a − + [ sin ⁡ − 1 ( x a ) − ln ⁡ ∣ x a + x 2 a 2 + 1 ∣ ] − a + 0 =\Big[\ln\Big|\frac{x}{a}+\sqrt{\frac{x^2}{a^2}-1}\Big|-\ln\Big|\frac{x}{a}+\sqrt{\frac{x^2}{a^2}+1}\Big|\Big]_{-\infty}^{-a^-}+\Big[\sin^{-1}\Big(\frac{x}{a}\Big)-\ln\Big|\frac{x}{a}+\sqrt{\frac{x^2}{a^2}+1}\Big|\Big]_{-a^+}^0

= ( ln ⁡ ∣ 1 ∣ − ln ⁡ ∣ 2 − 1 ∣ ) − ln ⁡ ∣ 1 a + 1 a 2 − 1 ( − ∞ ) 2 1 a + 1 a 2 + 1 ( − ∞ ) 2 ∣ + ( 0 − ( − π 2 ) ) − ( ln ⁡ ∣ 1 ∣ − ln ⁡ ∣ − 1 + 2 ∣ ) =(\ln|1|-\ln|\sqrt{2}-1|)-\ln\Big|\frac{\frac{1}{a}+\sqrt{\frac{1}{a^2}-\frac{1}{(-\infty)^2}}}{\frac{1}{a}+\sqrt{\frac{1}{a^2}+\frac{1}{(-\infty)^2}}}\Big|+(0-(-\frac{\pi}{2}))-(\ln|1|-\ln|-1+\sqrt{2}|)

= π 2 =\frac{\pi}{2}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...