Nasty Triangle

Geometry Level 1

The diagram above shows a triangle, it is known that $ADEF$ is a parallelogram, $X$ is a point on line $AB$ , $Y$ is a point on line $AC$ . If the area of $\triangle XEF$ is 1, then the area of $\triangle DEY$ is...

This is one part of 1+1 is not = to 3 .

The answer is 1.

3 solutions

Esrael Santillan
Jul 22, 2014

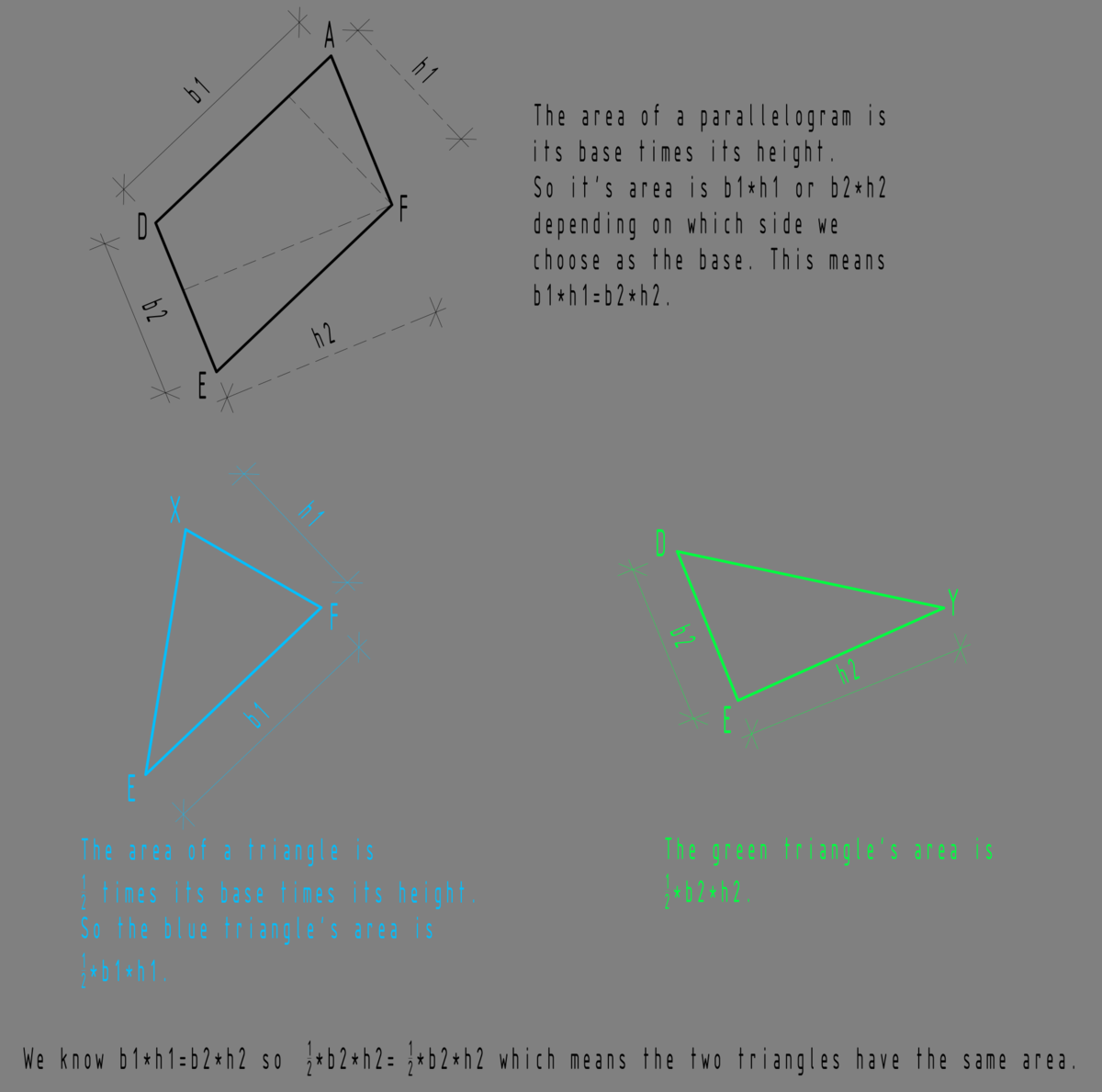
If you get the area of a triangle using calculus, you will notice that moving the top point horizontally will not change the area of the triangle. Also the area of triangle is $base \times height / 2$ so moving the top point along the line parallel to its base will neither change the $base$ nor the $height$ so the area will still be the same.

Let $EF$ be the based line.
Since $DA$ is parallel to $EF$ moving $X$ along $DA$ will not changed the area of $\triangle XEF$ .
Also $AC$ is parallel to $DE$ . Moving $Y$ along $AC$ will not changed the area of $\triangle DEY$ .
If you move Y in the location of F and move X in the location of D, then $\triangle XEF = \triangle DEY$ .

Therefore, $\triangle DEY$ has the same area with $\triangle XEF$ .

So the area of $\triangle DEY$ is also $\boxed 1$ .

But, where it is stated that any line is perpendicular to any other line??? How could you use that general triangle area formula then??? I think data is not sufficiently provided here

VAIBHAV borale - 6 years, 10 months ago

Perpendicular distances between 2 parallel lines are equal.

Each of these triangles = 1/2 the area of the parallelogram.

Guiseppi Butel - 6 years, 10 months ago

It is stated in the problem that $ADEF$ is parallelogram. About the triangle formula: Imagine 2 different triangles with the same base and height. Imagine their base are along x-axis. The only different between the two is the position of their topmost corner. If you move them horizontally parallel to their bases, the height will not changed. Since the area of triangle is $based \times height$ , moving their topcorner does not change neither $base$ nor the $height$ so the area will also not change.

Esrael Santillan - 6 years, 10 months ago

Chetan Chaurasia
Dec 25, 2017

Join DF. Area of DEF=EFX(between same parallel DX and EF line) Area of DEY=DFE(between same parallel AC and DE) Area∆EFX=area∆DEY=1 cm^2

S Broekhuis
Jan 27, 2021

Nasty Triangle

This is one part of 1+1 is not = to 3 .

The answer is 1.

3 solutions

0 pending reports