Nasty Triangles 2
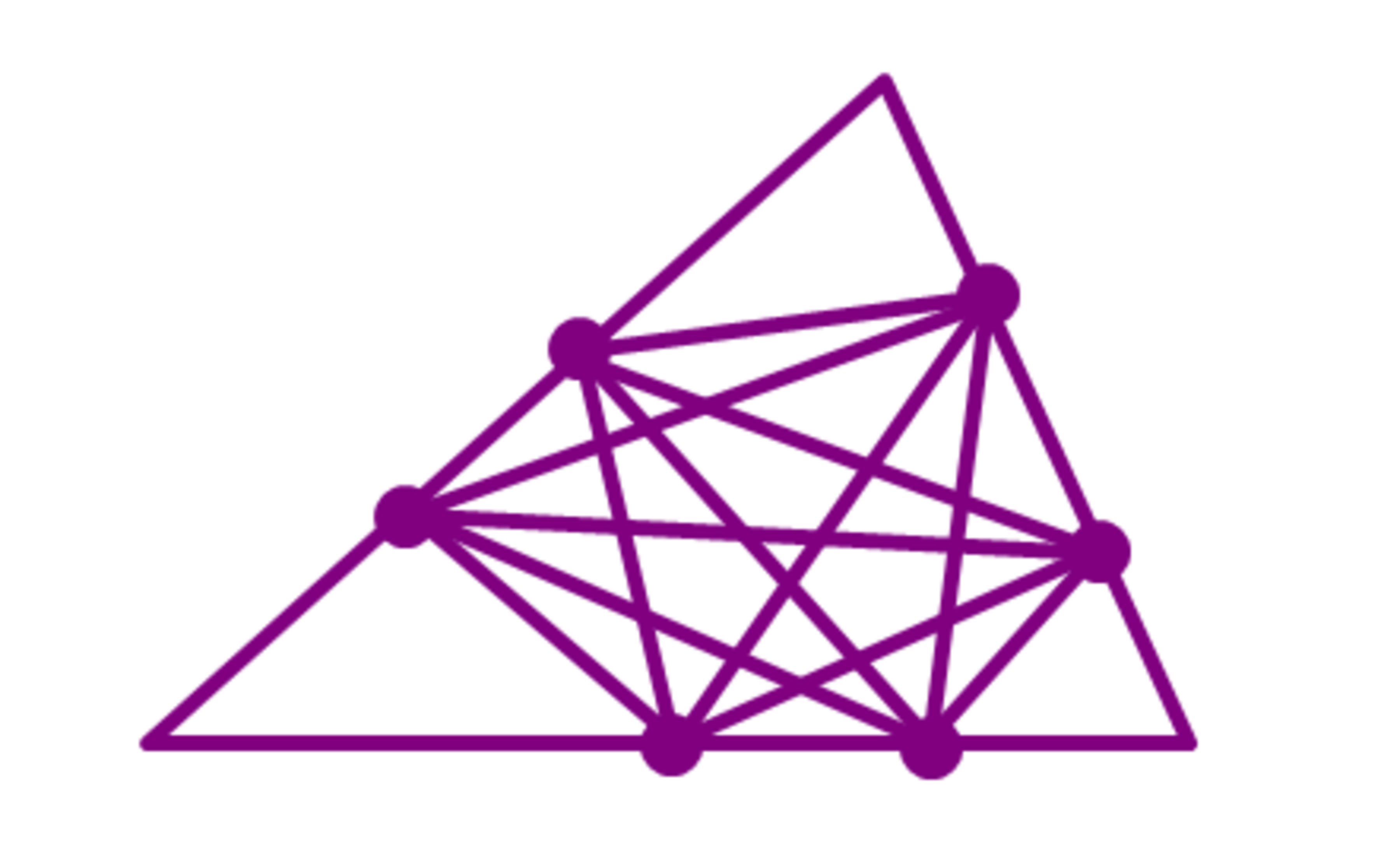
The diagram above shows another triangle. There are points on every side of this triangle, between every 2 points (both points are on different sides) there is a line connecting them, these lines will split the triangle into portions and no three lines intersect at 1 point. The above diagram shows an example of which will split the triangle into 28 portions, if , what is the total number of portions?
Also try Nasty Triangles 3 .
This is one part of 1+1 is not = to 3 .
The answer is 19876.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We will solve this problem by using combinations, we need to count the total number of lines and intersection points formed by all the lines before we can count the number of portions.
Let's first count the number of lines .
To draw a line, first we need to choose one of the sides of the triangle, there are ( 1 3 ) = 3 ways to choose a side. Then, on this side you've just chosen, from all the n points we need to choose 1, there are ( 1 n ) = n ways to do this. Now we need to choose another line, 2 sides remaining, so you have ( 1 2 ) = 2 ways to choose the second side, on that side you have ( 1 n ) = n ways to choose another point, connect the 2 points you've chosen and you have now formed a line! So, the total number of lines is 2 3 × n × 2 × n = 3 n 2 .
Now let's count the number of intersection points formed by the 3 n 2 lines,
since in every 4 points you can form a quadrilateral which has 2 diagonals forming an intersection point, the number of intersection points is equivalent to the number of quadrilaterals. So we just need to count the number of quadrilaterals. Let's split into 2 conditions.
(1) 2 vertices of the quadrilateral on one side and 2 vertices on another side.
To form this kind of quadrilateral, we'll choose a side, there are ( 1 3 ) = 3 ways to do this, next on this line, from n points we choose 2, which has a total of ( 2 n ) = 2 n ( n − 1 ) ways, then we choose the second side, with a total number of ( 1 2 ) = 2 ways, on that side we have ( 2 n ) = 2 n ( n − 1 ) ways to choose 2 points. Now we have 3 × 4 n 2 ( n − 1 ) 2 × 2 × 2 1 = 4 3 n 2 ( n − 1 ) 2
(2) 2 vertices of the quadrilateral on one side and 1 vertex on 2 other sides.
To form this kind of quadrilateral, first we choose a side, we can choose a side in ( 1 3 ) = 3 ways, then we can choose 2 points in ( 2 n ) = 2 n ( n − 1 ) ways, then we can choose another side in ( 1 2 ) = 2 ways, on that side we can choose a point in ( 1 n ) = n ways, finally we choose the last side in ( 1 1 ) = 1 way, on that side we can again choose a point in ( 1 n ) = n ways. Now we have 3 × 2 n ( n − 1 ) × 2 × n × 1 × n × 2 1 = 2 3 n 3 ( n − 1 )
Therefore, the total number of intersection points is 4 3 n 2 ( n − 1 ) 2 + 2 3 n 3 ( n − 1 ) = 4 3 n 2 ( n − 1 ) ( 3 n − 1 )
Now we have the total number of lines and intersection points, we can start counting the number of portions, how do we do this?
Let's assume one of the lines in the triangle intersects with k lines, forming k intersection points, these k lines will cut this line into k + 1 parts, each part of the line is a common boundary of 2 adjacent portions.
If we delete this line, these pairs of adjacent portions will join together into 1, which means the number of portions is decreased by k + 1 , continue deleting the other lines until all lines are deleted, we will only have 1 portion left (which is the triangle itself).
Reverse the process above, we add the lines one by one, if the added line intersects with k lines, forming k intersection points, the number of portions will increase by k + 1 , the sum of all the k 's is the the total number of intersection points we already know is 4 3 n 2 ( n − 1 ) ( 3 n − 1 ) , while the total number of lines is 3 n 2 , hence, the total number of portions is 3 n 2 + 4 3 n 2 ( n − 1 ) ( 3 n − 1 ) + 1
Now if we substitute n = 1 0 we could get 3 n 2 + 4 3 n 2 ( n − 1 ) ( 3 n − 1 ) + 1 = 1 9 8 7 6 .