Nasty Triangles 5
 Given
△
A
B
C
,
A
D
and
B
E
are angle bisectors of
∠
B
A
C
and
∠
A
B
C
respectively, if
A
B
=
2
1
,
B
C
=
2
4
,
A
C
=
1
5
, find the length of
D
E
2
.
Given
△
A
B
C
,
A
D
and
B
E
are angle bisectors of
∠
B
A
C
and
∠
A
B
C
respectively, if
A
B
=
2
1
,
B
C
=
2
4
,
A
C
=
1
5
, find the length of
D
E
2
.
This is one part of 1+1 is not = to 3 .
The answer is 84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
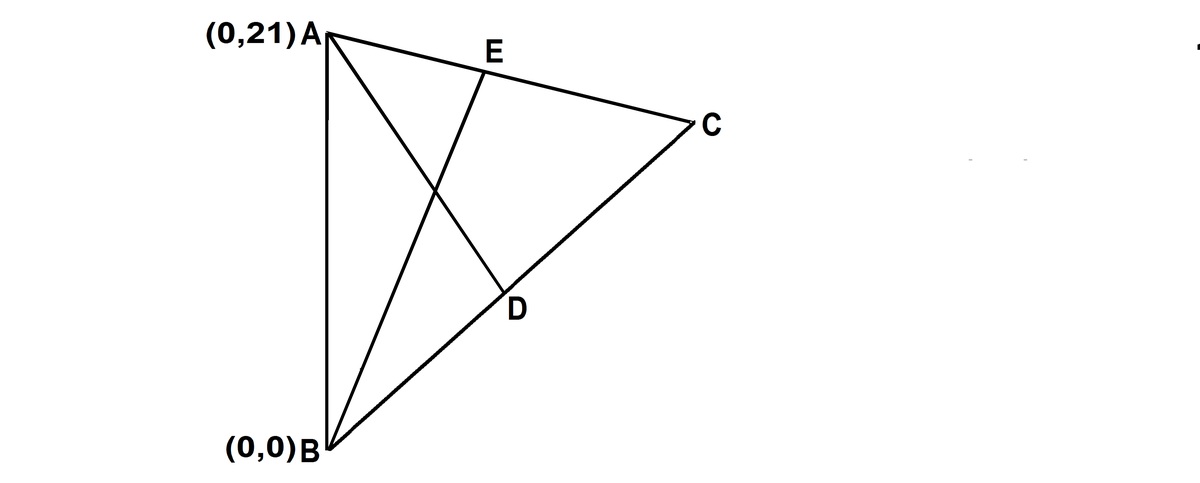 Above sketch is drawn shows the triangle in coordinate plane.
By Law of Cos,
∠
A
=
C
o
s
−
1
2
∗
2
1
∗
1
5
2
1
2
+
1
5
2
−
2
4
2
=
8
1
.
7
8
6
8
o
.
∠
B
=
C
o
s
−
1
2
∗
2
1
∗
2
4
2
1
2
+
2
4
2
−
1
5
2
=
3
8
.
2
1
3
2
o
.
∴
Y
B
C
=
T
a
n
(
9
0
−
B
)
∗
X
=
1
.
2
7
∗
X
,
Y
A
C
=
T
a
n
(
A
−
9
0
)
∗
X
=
−
1
.
4
1
∗
X
+
2
1
.
Y
B
E
=
T
a
n
(
9
0
−
2
B
)
∗
X
=
2
.
8
8
∗
X
,
Y
A
D
=
T
a
n
(
2
A
−
9
0
)
∗
X
=
−
1
.
1
5
∗
X
+
2
1
.
∴
S
o
l
v
i
n
g
f
o
r
D
X
a
n
d
D
Y
=
1
.
2
7
∗
D
X
,
D
(
8
.
6
6
,
1
1
)
.
S
o
l
v
i
n
g
f
o
r
E
X
a
n
d
E
Y
=
2
.
8
8
∗
E
X
,
E
(
6
.
9
8
,
2
0
)
.
∴
D
E
2
=
(
2
0
−
1
1
)
2
+
(
6
.
9
8
−
8
.
6
6
)
2
=
8
4
More accurate values were used on calculator to obtain integer 84.
Above sketch is drawn shows the triangle in coordinate plane.
By Law of Cos,
∠
A
=
C
o
s
−
1
2
∗
2
1
∗
1
5
2
1
2
+
1
5
2
−
2
4
2
=
8
1
.
7
8
6
8
o
.
∠
B
=
C
o
s
−
1
2
∗
2
1
∗
2
4
2
1
2
+
2
4
2
−
1
5
2
=
3
8
.
2
1
3
2
o
.
∴
Y
B
C
=
T
a
n
(
9
0
−
B
)
∗
X
=
1
.
2
7
∗
X
,
Y
A
C
=
T
a
n
(
A
−
9
0
)
∗
X
=
−
1
.
4
1
∗
X
+
2
1
.
Y
B
E
=
T
a
n
(
9
0
−
2
B
)
∗
X
=
2
.
8
8
∗
X
,
Y
A
D
=
T
a
n
(
2
A
−
9
0
)
∗
X
=
−
1
.
1
5
∗
X
+
2
1
.
∴
S
o
l
v
i
n
g
f
o
r
D
X
a
n
d
D
Y
=
1
.
2
7
∗
D
X
,
D
(
8
.
6
6
,
1
1
)
.
S
o
l
v
i
n
g
f
o
r
E
X
a
n
d
E
Y
=
2
.
8
8
∗
E
X
,
E
(
6
.
9
8
,
2
0
)
.
∴
D
E
2
=
(
2
0
−
1
1
)
2
+
(
6
.
9
8
−
8
.
6
6
)
2
=
8
4
More accurate values were used on calculator to obtain integer 84.
Nice solution, but actually this problem can be solved without using a calculator
I did the same but due to calculation mistake my answer came 81.pls suggest any other metho.
By law of cosines: A B 2 = A C 2 + B C 2 − 2 A C × B C cos C 2 1 2 = 1 5 2 + 2 4 2 − 2 × 1 5 × 2 4 cos C 4 4 1 = 2 2 5 + 5 7 6 − 2 × 1 5 × 2 4 cos C 2 × 1 5 × 2 4 cos C = 8 0 1 − 4 4 1 = 3 6 0 cos C = 2 1 ∴ ∠ C = 6 0 ∘ Since A D is the angle bisector of ∠ B A C , we have A C A B = D C B D D C B D = 5 7 B D + D C = B C = 2 4 ∴ B D = 1 4 , D C = 1 0 Since B E is the angle bisector of ∠ A B C , we have B C A B = E C A E E C A E = 8 7 A E + E C = A C = 1 5 ∴ A E = 7 , E C = 8 Now, by law of cosines, we could find the length of D E 2 : D E 2 = E C 2 + D C 2 − 2 E C × D C cos C = 8 2 + 1 0 2 − 8 × 1 0 = 1 6 4 − 8 0 = 8 4