7 Naughty Ducklings
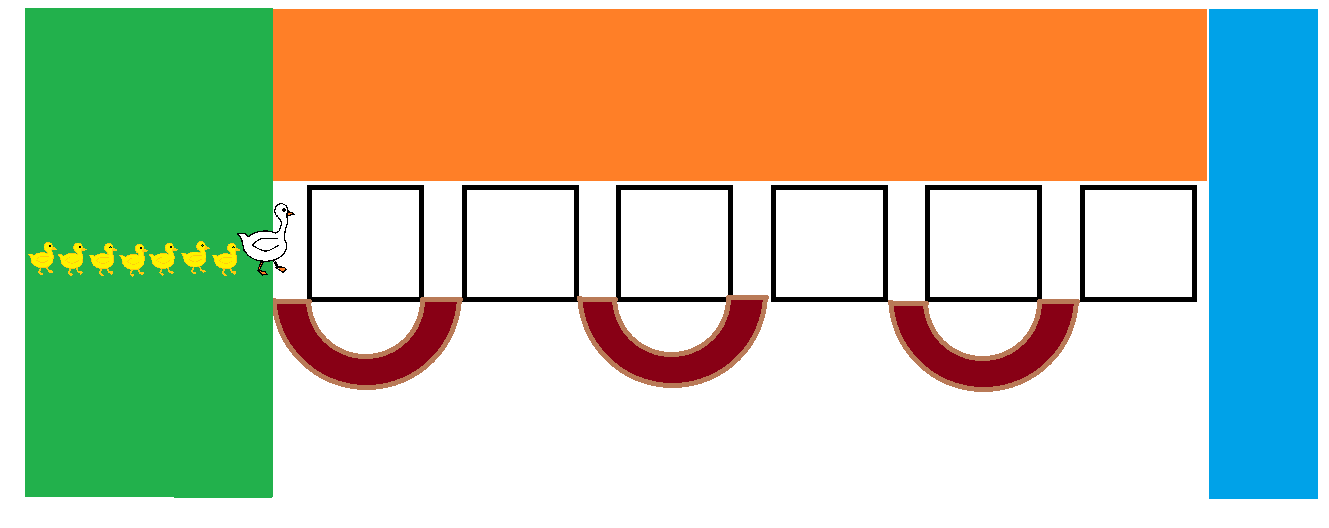
Once upon a time, there were 7 naughty ducklings, following their mother duck, treading from the green lawn towards the clear river ahead. Along their paths, there lay 6 clean white stone squares, besides the big orange barn. Even though the mother duck never walked astray from the stone pavement, her children often wandered off through the muddy alleys between each stone squares, as shown above.
After getting their feet dirty, they would leave their dark footprints or "dirt trail" on each stone square randomly. However, despite their childish play, they still kept up with their mother duck's pacing and never ran backwards, and after stepping over 2 square stones, their feet would get dry and would no longer leave any more mark, unless they dampened their feet off track again. Then after hopping into the river, their feet would be cleaned off by the water.
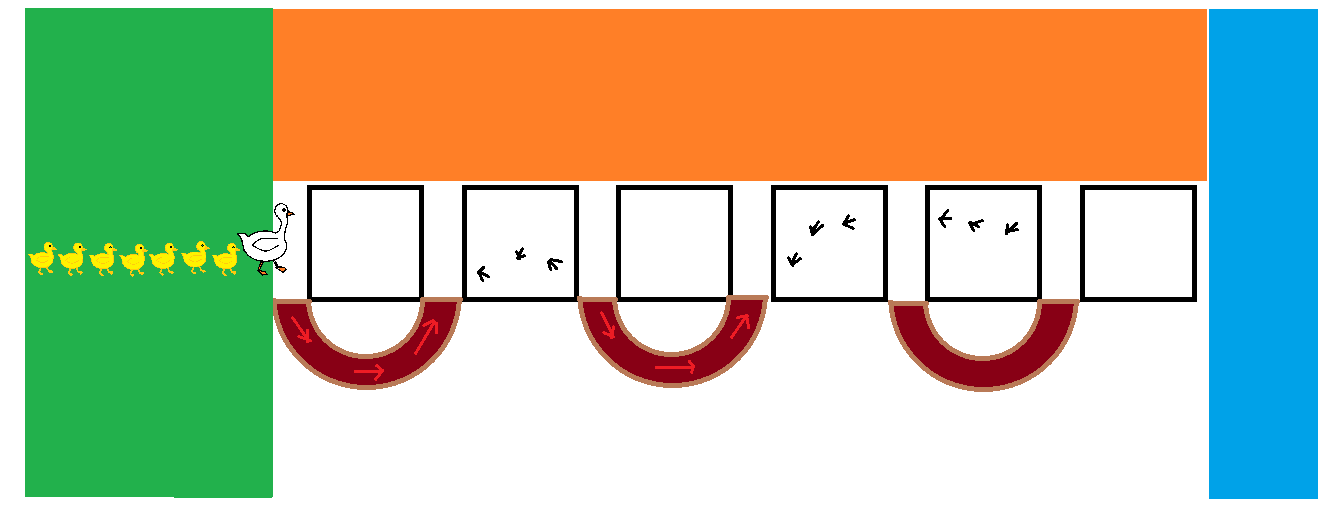
As an explicit example, if one duckling went off on the first and second muddy ways, it would leave 3 "dirt trails" on the second, fourth, and fifth stones, as shown above.
If every duckling had different paths from one another and there were 15 dirt trails in total, how many dirt trails were there on each stone, omitting the first one?
(For example, if you think there are 1,2,3,4,5 dirt trails on the second, third, fourth, fifth, & sixth stones respectively, enter 12345 as your answer.)
The answer is 42423.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each duck can choose between 2 choices (stone or path) in 3 places, for a total of 2 3 = 8 different ways. The following table shows these 8 different ways and the resulting dirt trails:
For example, the first row of the table shows a duck that chooses stone, stone, stone (SSS), and the result is no dirt trails on any of the stones, but the second row of the table shows a duck that chooses stone, stone, path (SSP), and the result is no dirt trails until the sixth stone, for a total of 1 dirt trail.
If there were 8 ducks choosing all different paths, there would be 1 6 dirt trails total. However, we are given that there are only 7 ducks with 1 5 dirt trails, so we must eliminate the only row on the table in which a duck would leave 1 dirt trail:
Therefore, there are 4 dirt trails on the second stone, 2 on the third stone, 4 on the fourth stone, 2 on the fifth stone, and 3 on the sixth stone, for an answer of 4 2 4 2 3 .