Naughty jaywalkers

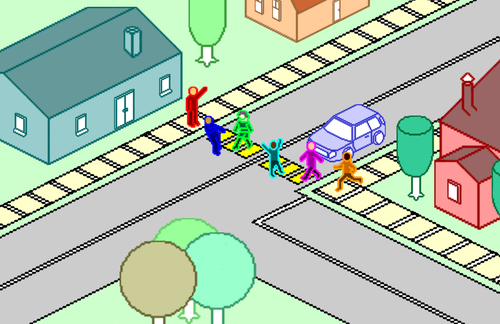The good thing about jaywalking is that it's less illegal than manslaughter.

Taking advantage of this, a pedestrian who doesn't have a crossing signal can (illegally) enter a crosswalk before an approaching car breeches the crosswalk. Not wanting to kill the pedestrian, the car is forced to wait for the pedestrian to pass, even though the driver has the right of way. This opens up a jaywalking window. If a second pedestrian enters the crosswalk before the first pedestrian passes the end of the car, the jaywalking window is extended until the second pedestrian passes the end of the car.

If no new pedestrian enters the crosswalk before the last pedestrian to enter the crosswalk reaches the end of the car, the jaywalking window is closed and the car can proceed.

Suppose a stream of pedestrians emerges from a subway station, and walk down the sidewalk with constant speed, toward the crosswalk. The first pedestrian enters the crosswalk (without a crossing signal), just ahead of a car, opening a jaywalking window. The subsequent pedestrians follow suit, always entering the crosswalk if the jaywalking window is open.

Question : How many pedestrians are able to cross in the average jaywalking window?

Assumptions

• The distance $d$ (as shown in the diagram), from the curb to the end of the car is $\text{1.8 m}$
• The pedestrians emerge at random from the subway such that there is an average of $\rho = \text{2.5 pedestrians per meter}$

---

Figures by Maxicat Rhododendron