Neat identity
Consider a square with side length k = 1 ∑ n k and a solid consisting of n cubes with side lengths 1 , 2 , 3 , . . . , n respectively.
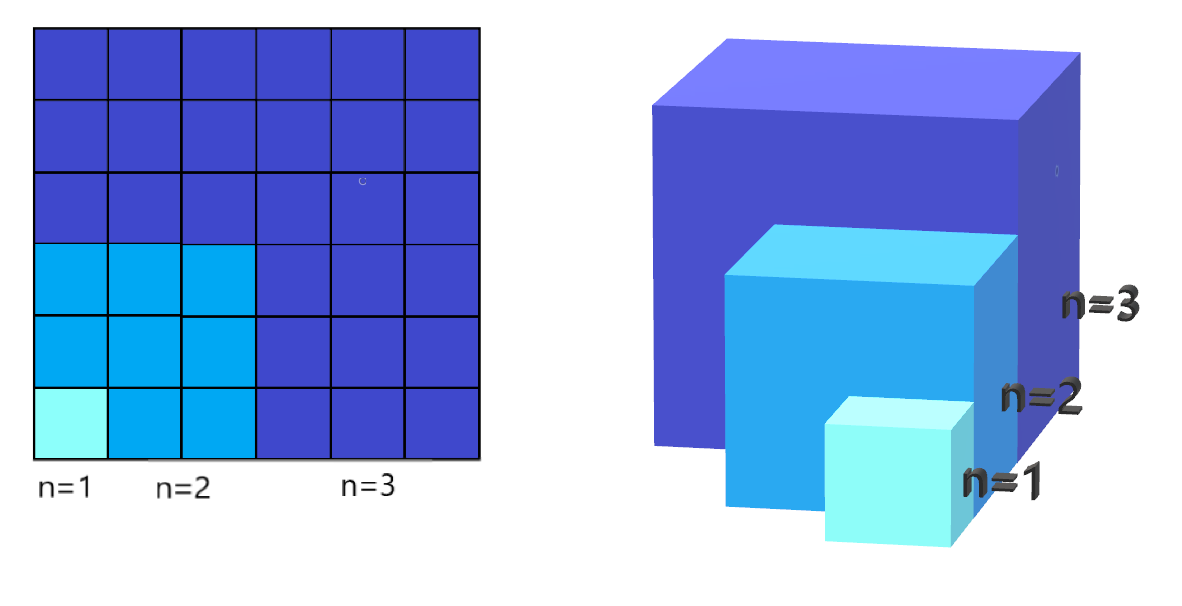
What is the ratio between the area of the square and the volume of the solid, when n = 2 7 ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The main condition is n = 2 7
S i d e o f t h e s q u a r e ( s ) = k = 1 ∑ n = 2 7 k = 2 n ( n + 1 ) = 2 2 7 × 2 8 = 3 7 8
Now, A r e a o f t h e s q u a r e = s 2 = ( 3 7 8 ) 2
To obtain the volume of resulting solid we have to add all the volumes of the individual cubes.
V o l u m e o f t h e f i n a l s o l i d = 1 3 + 2 3 + 3 3 + . . . . . + 2 7 3 ( o r ) k = 1 ∑ n = 2 7 k 3
⟹ 4 n 2 ( n + 1 ) 2 = 4 2 7 2 × 2 8 2 = ( 3 7 8 ) 2
Now, Ratio = Volume of the solid Area of the square = ( 3 7 8 ) 2 ( 3 7 8 ) 2
⟹ 1 : 1
Once you play a little with the numbers, it's quite easy to notice that no matter what n is equal to, the result is always 1 . This would mean that ( k = 1 ∑ n k ) 2 = k = 1 ∑ n k 3 .
Now let's consider n = 2 . If we were to increase the side length of the square by 3 now, it should add as much area to our square as volume to our solid if the above statement is true. That means that the dark blue coloured area should be equal to the volume of the dark blue coloured cube.
Remember that we can write k = 1 ∑ n k as 2 n ( n + 1 ) .
This way we can express the dark coloured area as A = ( 2 n ( n + 1 ) ) 2 − ( 2 ( n − 1 ) n ) 2 .
( 2 n ( n + 1 ) ) 2 − ( 2 ( n − 1 ) n ) 2 = 4 ( n 2 + n ) 2 − ( n 2 − n ) 2 = 4 ( n 4 + 2 n 3 + n 2 ) − ( n 4 − 2 n 3 + n 2 ) = 4 4 n 3 = n 3
I don't need to tell you, that the volume of the dark coloured cube is also n 3 , so this identity holds true.