Need to draw, Part 2

Solution using coordinate geometry:

Let the medians intersect at the origin.

AD is on the x-axis and BE is on the y-axis.

$A=(-a,0)$ and $B=(-b,0)$

Since AD and BE are medians, if A is a units to the left of the y-axis, then C is a units to the right. Similarly, C is b units above the x-axis.

$C=(a,b)$

By Pythagoras' Theorem, $a^2+4b^2=9$ $4a^2+b^2=16$

Adding both equations and dividing by 5, $a^2+b^2=5$ $\Rightarrow AB=\sqrt{5}$

Solution using trigonometry:

Let $G$ be the centroid of $\Delta ABC$ and $F$ be the midpoint of $AB$ .

As $AD \perp BE$ , $F$ is the circumcentre of (right) $\Delta ABG$ . $\implies \frac{AB}{2}=AF=FB=FG \implies CF=\frac{3}{2} AB$

Now, we have the following equations (which hold in general): $\begin{aligned} 4\cdot CF^2&=AC^2+BC^2+2AC\cdot BC\cdot \cos \angle BCA\\AB^2&=AC^2+BC^2-2AC\cdot BC\cdot \cos \angle BCA\end{aligned}$

Now, using the above three equations and the given values, we have

$AB=\boxed{ \sqrt5}$

Mine was a vector approach! I considered $B$ at the origin and side $BC$ along the x-axis.

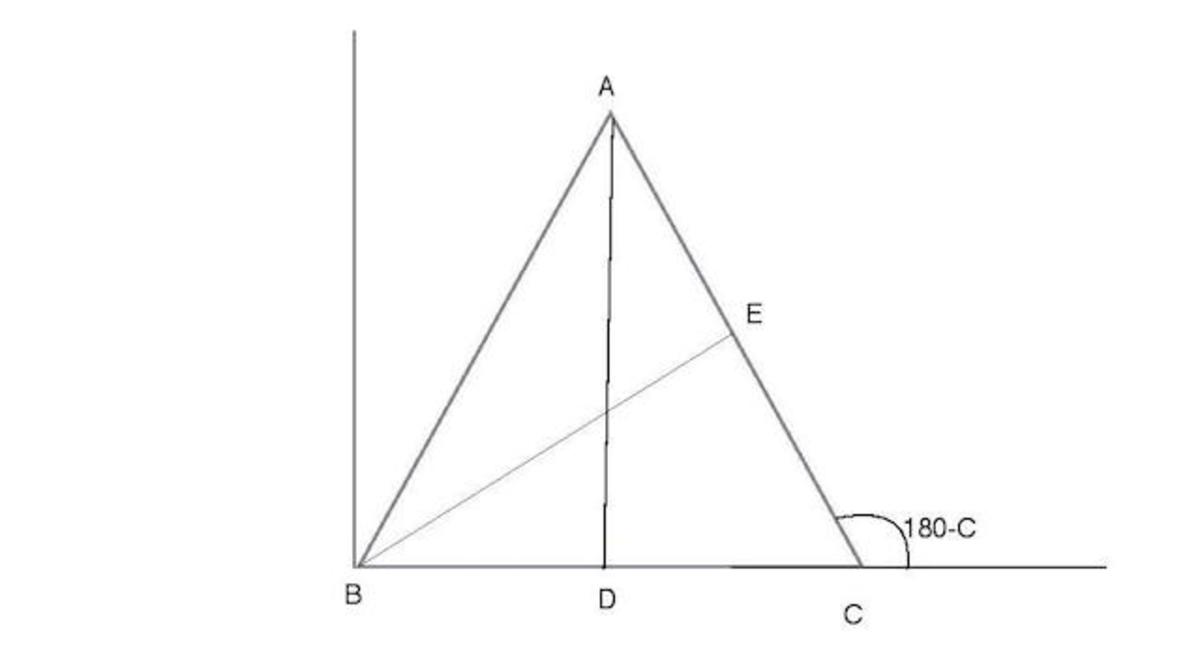
The idea is to find $\vec{BE}$ and $\vec{AD}$ and then use the fact that $\vec{BE}.\vec{AD}=0$ since, the medians are perpendicular.

Let $O$ denote the origin. Therefore, from the diagram we can write:

• $\vec{OB} = \vec{0}$

• $\vec{BC} = 3\hat{i}$ ( length BC = $3$ cm )

• $\vec{BD} = \frac{3}{2}\hat{i}$

Now the task is to find $\vec{AD}$ and $\vec{BE}$ .

From Triangle Law of Addition of Vectors we can write :

$\vec{BC} + \vec{AC}=\vec{BA}$

But $\vec{AC} = -4cosC\hat{i} + 4sinC\hat{j}$

Therefore $\vec{BA} = \left(3-4cosC\right)\hat{i}+4sinC\hat{j}$

But our aim is to find $\vec{AD}$ .

$\vec{AD}=\vec{BA}-\vec{BD} \Rightarrow \boxed{\vec{AD}=\left(\frac{-3}{2}+4cosC\right)\hat{i}-4sinC\hat{j}}$

Similarly $\vec{BE} = \vec{BC}+ \vec{EC} \Rightarrow \boxed{\vec{BE} =\left(3-2cosC \right)\hat{i}+2sinC\hat{j}}$

Now using the given information- $\vec{AD}.\vec{BE}=0$ we get:

$\boxed{cosC=\frac{5}{6}}$

Now we can apply Cosine Rule upon using which we get

$AB =\large \boxed{\sqrt{5}}$