Needs a elegant solution apart from hit and trial (2)

$x+\sqrt{y}=27\Rightarrow x=27-\sqrt{y}...(1)$ $y+\sqrt{x}=9\\ \Rightarrow x=(y-9)^2$ $\Rightarrow 27-\sqrt{y}=y^2-18y+81~~(\text{Using (1)})$ Let $\sqrt {y}=t$ $\Rightarrow t^4-18t^2+t+54=0\\ \Rightarrow (t-2)(t^3+2t^2-14t-27)=0$ $\Rightarrow \sqrt {y} =t=2~\color{#302B94}{(**)}$ $\Rightarrow y=4 ,x=27-\sqrt{y}=25$ $\Large 25+4=\huge\boxed{\color{#007fff}{29}}$

---

$\color{forestgreen}{\boxed{\color{#302B94}{**\text{Further Analysis}}}}$

Let f(t)= $t^3+2t^2-14t-27$ . Knowing the fact that t>0(since t= $\sqrt{y}$ ), we have to look only for positive integral t's. Since for t>0 $t^3+2t^2-14t-27=0$ for only t∈(3,4){Apply Intermediate Value Theorem } and in this interval we cannot get any integral t and hence no integral y.

Though the answer can be obtained by hit and trial , I give a formal way of solving this beautiful problem:

Since $x$ is an integer and from first equation $\sqrt{y}=27-x$ , this means $\sqrt{y}$ is an integer and $y$ is a perfect square. Similarly from second equation we can deduce $x$ is a perfect square as well.

So we let $x=a^2$ , $y=b^2$ for some integers $a,b$ . Now the system of equations we are going to solve transform to:

$a^2+b=27 \dots (1) \\ b^2+a=9 \dots (2)$

From $(2)$ , we have $a=9-b^2 \dots (3)$ and substituting this in $(1)$ , we have :

$(9-b^2)^2+b=27 \Rightarrow 81-18b^2+b^4+b=27 \Rightarrow b^4-18b^2+b+54=0$

By rational root theorem , we see that $b=2$ satisfies the above equation and hence we factorize like this:

$b^4-18b^2+b+54= (b-2)(b^3+2b^2-14b-27)$

By rational root theorem we can show that $(b^3+2b^2-14b-27)=0$ does not have integer solution and hence the only permissible solution is $b=2$ . Substituting $b=2$ in $(3)$ , $a=9-2^2=9-4=5 \Rightarrow a=5 \ , \ b=2$ .

Hence , $x=5^2=25 \ , \ y=2^2=4 \Rightarrow \boxed{x+y=29}$ .

If we set $\sqrt{x}=t;\sqrt{y}=u$ then we'll have $t,u\geq 1$ $\begin{cases} t^2+u=27 (1)\\ u^2+t=9 (2)\end{cases}$ So (1)-(2)=18 $\Leftrightarrow t^2 - u^2 - (t-u)=18$ $\Leftrightarrow (t-u)(t+u-1)=18$ We see that $t+u-1\geq 1>0\Rightarrow t>u$ and $t-u< t+u-1$ .Therefore $t-u$ and $t+u-1$ must be positive divisor of 18 since two of them are positive integers. Based on (1) and (2), we also knows that $t\leq 5$ , $u\leq 2$ cause x, y must be square numbers

Now we have this table 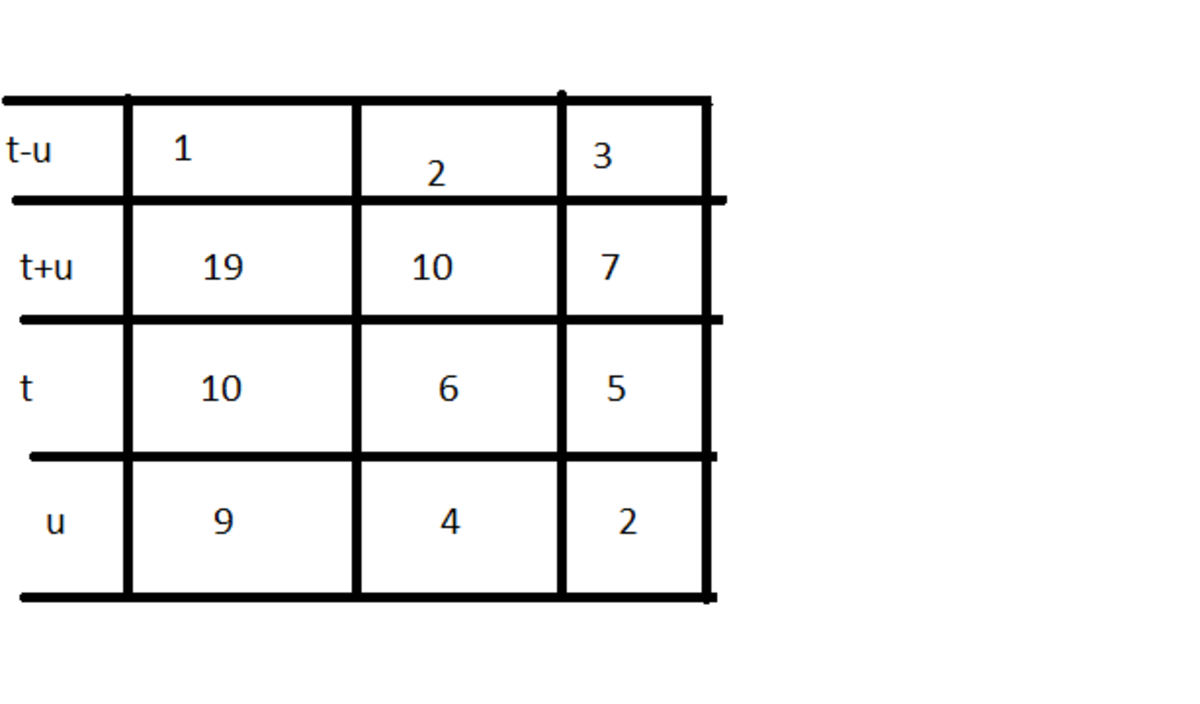Clearly see that $(t;u)=(5;2)$ satisfy the condition so $x=25;y=4 \Rightarrow x+y=29$