Neither series nor parallel circuit
Five resistors are connected as shown below.
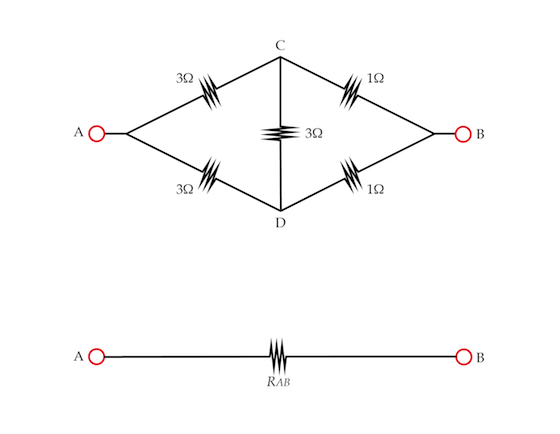
Note that the resistors are neither connected in series nor in parallel. However, it turns out that the set of resistors is equivalent to a single resistor R A B . Determine the resistance in Ohms R A B .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Discussions for this problem are now closed
Notice that, this arrangement forms a balanced Wheatstone bridge. So you can easily remove the connecting resistance and this arrangement simplifies to a series and parallel connection.
For more information on Wheatstone bridge, watch this video:
yep. this circuit is way more simple than what it appears at first.
here we should consider the wheatstone bridge in which the current flowing through the CD bridging resistor to be zero, as the bridge is balanced.i.e p/q=r/s here p=r=3 ohms and q=s=1 ohm. p and q are in series and so are q and s. the combination of p and q is in parallel with that of s and r.i.e equivalent resistance of the combination will be (p+q)(r+s)/p+q+r+s= 2 ohms
We have the following equations:
v a − v c = 3 i
v a − v d = 3 ( I − i )
v c − v d = 3 j
v c − v b = i − j
v d − v b = I − i + j
Solving, we have j = I − 2 i and i = 2 1 I . Finally, we have v a − v b = 2 I ⟹ I v a − v b = 2 .
using delta to wye convertion, Ry = Rdelta/3, for balanced resistances. then converting the left side with 3 ohms, Ry = 1 ohm.
after that, two-1 ohm are in series and in parallel to the same two-1 ohm resistors, which is in series with the 1 ohm resistance on the left side. Rab = 1 + ((2*2)/(2+2)) = 2 ohms
Since this circuit is symmetrical about the x-axis, , there can be no current along the path C D .
So it is just the same as two resistors of 4 Ω in parallel, i.e. 2 Ω total.
However, if the circuit were not symmetrical then we could solve it via the Y-delta transform :
 my picture
my picture
This transform changes a triangle of resistors, into resistors going from each vertex to a point. The formula is given in the above link; in this case it works out that D P = 3 D C = 1 . So we end up with A P = 1 Ω , P C = P D = 1 Ω , and C B = D B = 1 Ω which are unchanged from the original.
The section from P to B is two parallel resistances of 2 Ω , so the total resistance from P to B is 1 Ω . Combining this in series with A P gives the total of 2 Ω .
hmmm... quite interesting. but a simple way could be that the potential drop across C and D is equal as they both cross a 3 ohm resistor. therefore the current will not flow through wire CD. this can be one of the approaches
The best way to do one of these is to 'connect' a 1V source to the outputs, solve the circuit using mesh analysis, and use Ohm's law on the remaining loop. From mesh analysis, we receive (naming the loops clockwise, starting from the left triangle):
9 I 1 − 3 I 2 − 3 I 3 − 3 I 1 + 5 I 2 − I 3 − 3 I 1 − I 2 + 4 I 3 = 0 = 0 = 1 Solving gives us, simply that ( I 1 , I 2 , I 3 ) = ( 4 1 , 4 1 , 2 1 ) , and, using Ohm's law, we have that: I V = R = . 5 1 = 2 Ohms
Try to observe,
This is a balanced Wheatstone bridge,
Hence, no current will flow from resistor CD of 3 ohm
total resistence in ACB = 4 ohm
total reisitence in ADB = 4 ohm
ADB and ACB are in parallel connection
Hence, total resistence = 4 + 4 4 × 4 ohms = 2ohms
The three 3 ohms resistors forms a delta which can be converted to three 1 ohms resistors in a star (since (3 3)/(3+3+3)=1. Delta to star conversion formula R1=(R12 R13)/(R12+R13+R23)), one of these three 1 ohm resistor in the star connects to point A and the other two connected to one each of the 1 ohms resistors connected to point B. The resultant is a circuit with a 1 ohm resistor in series with two parallel 2 ohms resistors (series circuit formula R=R1+R2+….). which is again equal to a circuit with a 1 ohm resistor in series with another 1 ohm resistor ( parallel circuit formula (1/R)=(1/R1)+(1/R2)+…..) ). The equivalent resistance is therefore 2 ohms.(series circuit formula R=R1+R2+….).