Nested n-gons
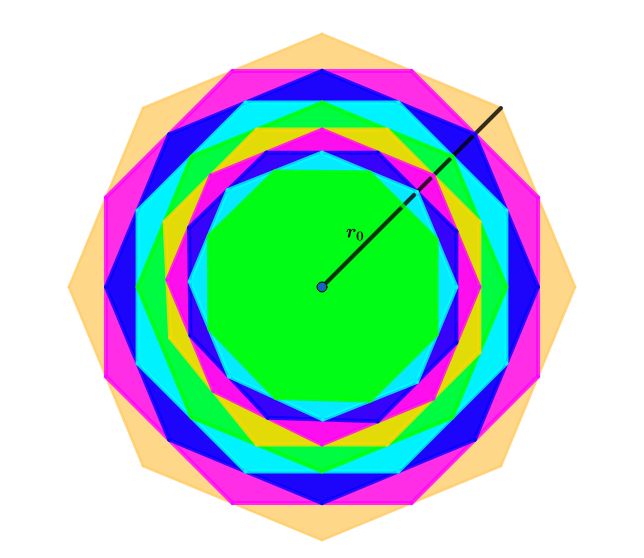
Extend the diagram above to an infinite number of inscribed n − g o n s ..
Let P j , n be the j t h regular n − g o n and P j + 1 , n be inscribed in P j , n , where each vertex of P j + 1 , n touches each midpoint of each side of P j , n .
For j ≥ 0 let A j , n be the area of j t h n − g o n ..
(1): If A n = ∑ j = 0 ∞ A j , n , find A 0 , n A n .
(2): Find A 0 , 1 0 0 A 1 0 0 to eight decimal places.
The answer is 1013.54523557.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
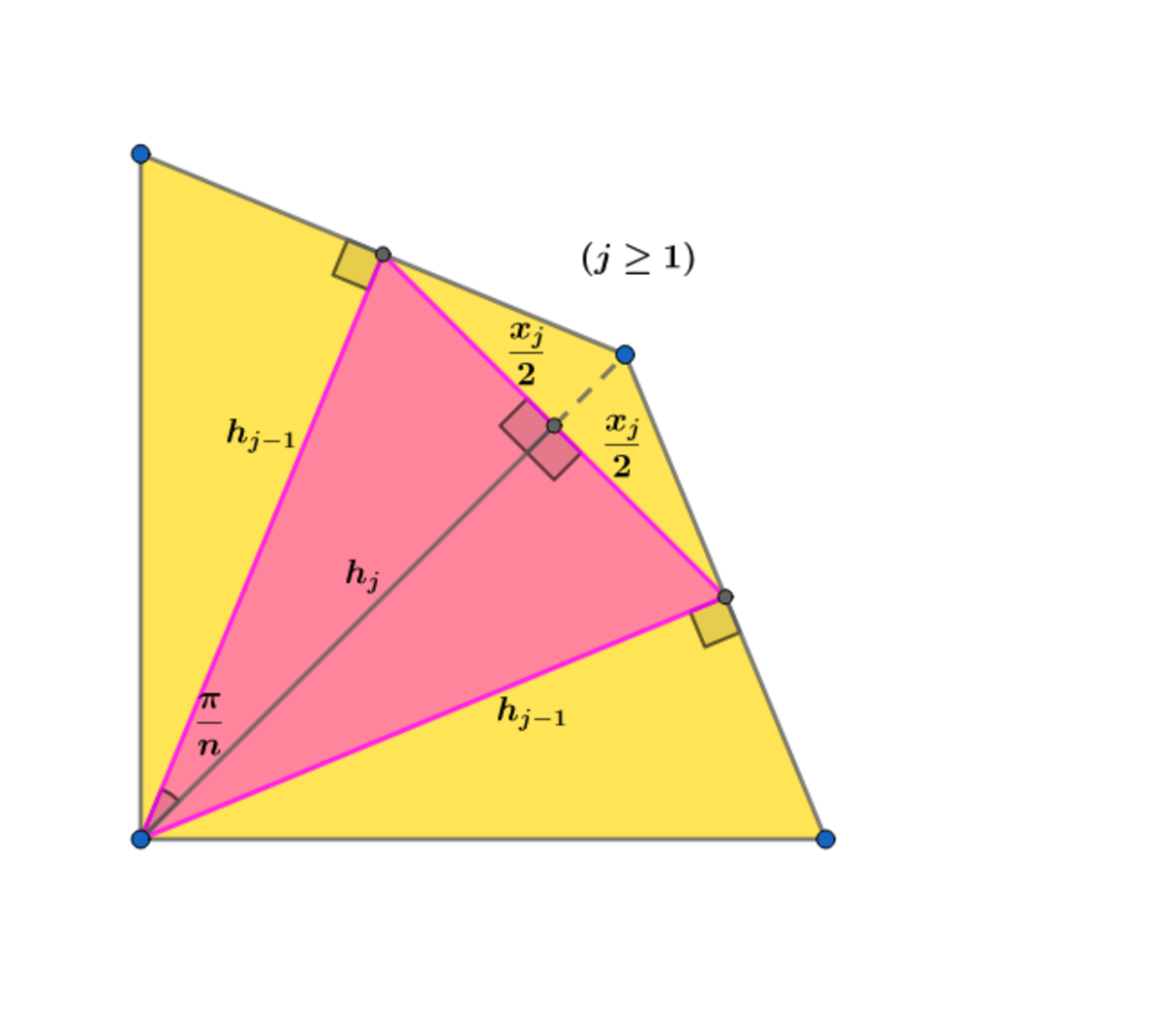
Let h 0 and x 0 be the height and a side of the initial n − g o n
then
x 0 = 2 r 0 sin ( n π ) and h 0 = r 0 cos ( n π )
⟹ h 1 = h 0 cos ( n π ) = cos 2 ( n π ) r 0 , x 1 = 2 h 0 sin ( n π ) = 2 cos ( n π ) sin ( n π ) r 0 = sin ( n 2 π ) r 0
⟹ h 2 = h 1 cos ( n π ) r 0 = cos 3 ( n π ) r 0 , x 2 = 2 h 1 sin ( n π ) = 2 cos 2 ( n π ) sin ( n π ) r 0 = sin ( n 2 π ) cos ( n π ) r 0
⟹ h 3 = h 2 cos ( n π ) = cos 4 ( n π ) r 0 , x 3 = 2 h 2 sin ( n π ) = sin ( n 2 π ) cos 2 ( n π ) r 0
and,
h j − 1 = cos j ( n π ) r 0 , x j − 1 = sin ( n 2 π ) cos j − 2 ( n π ) r 0
⟹ h j , n = cos j + 1 ( n π ) r 0 , x j , n = sin ( n 2 π ) cos j − 1 ( n π ) r 0
⟹ A j , n = 2 n cos 2 j ( n π ) sin ( n 2 π ) r 0 2 ⟹
A n = ∑ j = 0 ∞ A j , n = 2 n sin ( n 2 π ) r 0 2 ∑ j = 0 ∞ ( cos 2 ( n π ) ) j = sin 2 ( n π ) 2 n sin ( n 2 π ) r 0 2 = sin 2 ( n π ) A 0 , n ⟹ A 0 , n A n = sin 2 ( n π ) 1 ⟹ A 0 , 1 0 0 A 1 0 0 ≈ 1 0 1 3 . 5 4 5 2 3 5 5 7 .
Let C n denote the point about which all the regular n -gons are rotationally symmetric (Exercise: Prove that this point is well-defined), let V j , n denote a vertex of P j , n , and let V j + 1 , n denote one of the adjacent sides' midpoints (which by definition is one of the vertices of P j + 1 , n ). Then C n V j + 1 , n ⊥ V j , n V j + 1 , n , so by basic trigonometry, C n V j , n C n V j + 1 , n = cos ( ∠ V j , n C n V j + 1 , n ) = cos n π so that since all the n -gons are similar, A j , n A j + 1 , n = ( C n V j , n C n V j + 1 , n ) 2 = cos 2 ( n π ) . This ratio doesn't depend on j , so A j , n forms a geometric sequence with initial value A 0 , n and common ratio r = cos 2 ( n π ) . Since ∣ r ∣ < 1 , A n = j = 0 ∑ ∞ A j , n = 1 − cos 2 ( n π ) A 0 , n = sin 2 ( n π ) A 0 , n = A 0 , n csc 2 ( n π )
That is, A 0 , n A n = csc 2 ( n π ) ⟹ A 0 , 1 0 0 A 1 0 0 = csc 2 ( 1 0 0 π ) ≈ 1 0 1 3 . 5 4 5 2 3 5 5 6 4 3 8 2 9 8 6 4 8 5