Nested Cylinders and Cones

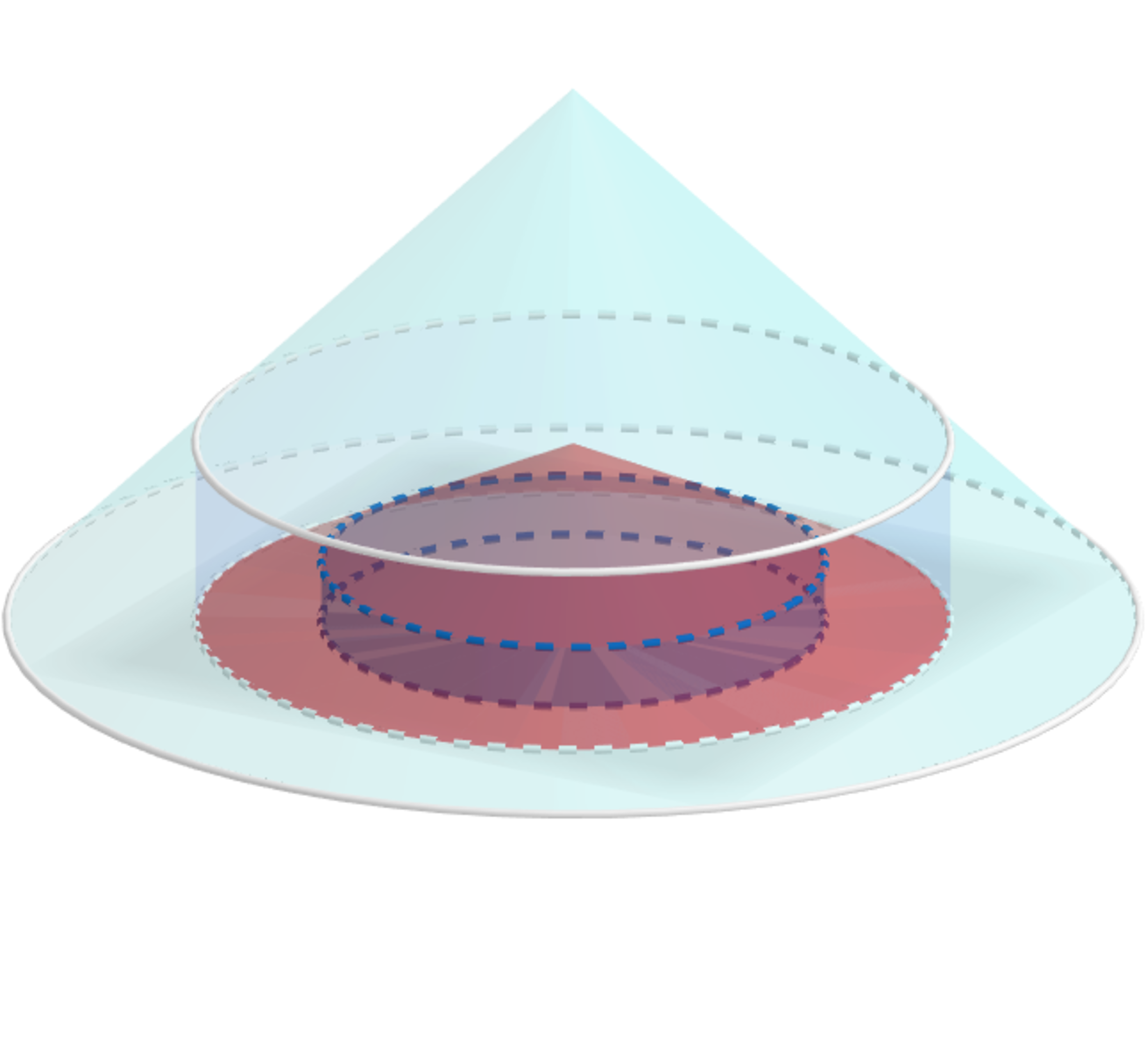
$V_{p}(1) = \dfrac{1}{3}\pi R_{1}^2H_{1}$ and $V_{c}(1) = \pi r_{1}^2h_{1}$

The two right triangles in the above diagram are similar $\implies \dfrac{R_{1} - r_{1}}{R_{1}} = \dfrac{h_{1}}{H_{1}} \implies h_{1} = \dfrac{R_{1} - r_{1}}{R_{1}}H_{1} \implies V_{c}(1) = \pi \dfrac{H_{1}}{R_{1}}(R_{1}r_{1}^2 - r_{1}^3) \implies$

$\dfrac{dV_{c}(1)}{dr_{1}} = \pi\dfrac{H_{1}}{R_{1}}r_{1}(2R_{1} - 3r_{1}) = 0 \implies r_{1} = \dfrac{2}{3}R_{1} \implies h_{1} = \dfrac{1}{3}H_{1}$

and $p(2)$ inscribed in $c(1)$ $\implies R_{2} = r_{1}$ and $H_{2} = h_{1}$

$\implies r_{2} = \dfrac{2}{3}R_{2} = \dfrac{2}{3}(\dfrac{2}{3})R_{1} = (\dfrac{2}{3})^2R_{1}, \:\ h_{2} = \dfrac{1}{3}H_{2} = \dfrac{1}{3}(\dfrac{1}{3})H_{1} = (\dfrac{1}{3})^2H_{1},$ $R_{3} = r_{2}, \:\ H_{3} = h_{2}, \:\ r_{3} = \dfrac{2}{3}(\dfrac{2}{3})^2 R_{1}, \:\ h_{3} = \dfrac{1}{3}(\dfrac{1}{3})^2$

In General:

$R_{n} = (\dfrac{2}{3})^{n - 1}R_{1}$

$H_{n} = (\dfrac{1}{3})^{n - 1}H_{1}$

$r_{n} = \dfrac{2}{3}(\dfrac{2}{3})^{n - 1}R_{1}$

$h_{n} = \dfrac{1}{3}(\dfrac{1}{3})^{n - 1}H_{1}$

$\implies$

$V_{p}(n) = \dfrac{1}{3}\pi R_{n}^2H_{n} = (\dfrac{4}{27})^{n - 1}V_{p}(1)$

and

$V_{c}(n) = \pi r_{n}^2h_{n} = \dfrac{4}{9}(\dfrac{4}{27})^{n - 1}V_{p}(1)$

$\implies$

$V_{p} = V_{p}(1)\sum_{n = 1}^{\infty} (\dfrac{4}{27})^{n - 1} = \dfrac{27}{23}V_{p}(1)$

and

$V_{c} = (\dfrac{4}{9})(\dfrac{27}{23}) = \dfrac{12}{23}V_{p}(1)$

$\implies \dfrac{V_{p} * V_{c}}{V_{p}(1)^2} = (\dfrac{3^2 * 2}{23})^2 = (\dfrac{a^b * b}{c})^b \implies a + b + c = \boxed{28}$ .