Nested Fractional Exponent Discovered

If we put $b = \tfrac12$ , then we have $a_0 \; = \; \tfrac12 \hspace{2cm} a_1 = \big(\tfrac12\big)^2 = \tfrac14 \hspace{2cm} a_2 = \big(\tfrac12\big)^4 = \tfrac{1}{16}$ and, in general $a_{n+1}^{-1} \; = \; 2^{a_n^{-1}}$ so that the $a_n^{-1}$ form a tetration tower, $a_n^{-1} \; = \; 2^{2^{2^{\cdot^{\cdot^{\cdot^2}}}}} \hspace{2cm} (n+1\; \text{copies of } 2)$ which diverge to $\infty$ , and hence $a_n \to 0$ as $n \to \infty$ , and (of course), $0$ is an integer.

The original question is basically to prove that the sequence $a_0 = b; \quad a_{n+1} = {\large b^{\frac{1}{a_n}} }$ converges to 2 when b = 4. From basic definition of the convergence of a sequence, we know that if $a_n$ converges, then $\lim_{n -> \infty} a_n ~~=~~ \lim_{n -> \infty} a_{n+1}~=~ L$ So, as $n -> \infty$ , it follows that the sequence formula becomes $L = b^{1/L}$ . Hence, raising both sides to power $L$ gives the expression $L^L ~=~ b$ .

Hence, for $b = 4$ , the sequence will converge to a value $L$ , provided $L^L = 4$ , from which it easily follows that $L = 2$

Based on the above, I would conjecture that the above sequence would converge if b = 27 ( $= 3^3$ ), or any other "self powered" value.

I'll try to prove it.

Let us assume that the sequence does coverge, to the value $a_\infty$ . Thus, $a_\infty=a_{\infty+1}=b^{\frac{1}{a_\infty}}$ , which means that $a_\infty^{a_\infty}=b$ (Sorry for the abuse of notation). Notice that for every $b>1,\ a_\infty>1$ this is a bijection, and $a_\infty<b$ thus we can find some $a_\infty$ that satisfies that condition.

Now lets prove that it must converge, that is to show that $Lim_{n \rightarrow \infty}|a_\infty-a_n|=0$ , for Can it be done?

It can be shown using induction on n that $a_{2n}>a_{2n+1},\quad a_{2n+2}<a_{2n},\quad a_{2n+1}>a_{2n-1}$ .

The sequences $a_{2n+1}$ and $a_{2n}$ must converge to some values between $a_0$ and $a_1$ , or otherwise at least one of the inequalities above will not hold.

WLOG assume that $Lim_{n \rightarrow \infty}a_{2n}=C$ , $b^\frac{1}{b}=a_1<C<a_0=b$ . It must hold that $C=b^{\frac{1}{b^{\frac{1}{C}}}}=b^{-b^{-\frac{1}{C}}}$ , thus $C^{b^{\frac{1}{C}}}=b$ .

To solve it, assume $b=C^d$ for some $1<d<b$ , i.e. $d=log_C(b)$ . It gives in the previous equation $C^{b^{\frac{1}{C}}}=C^d$ , thus $b^{\frac{1}{C}}=C^{\frac{d}{C}}=d$ that is $C^\frac{1}{C}=d^\frac{1}{d}$ . This is very tricky, as when C and d are both bigger than 1 there are two solutions: $C=d$ but also another non analytic solution where $1<C<e\ \rightarrow d>C$ and $C>e\ \rightarrow 1<d<C$ . Thus $b=C^C$ or $b=C^d=d^C$ .

For the sequence $a_{2n+1}$ we get the similar results - if $Lim_{n \rightarrow \infty}a_{2n}=K$ than $b=K^K$ or $b=K^p=p^K$ $(d'=log_K(b))$ .

If $b=C^C$ than $C=a_\infty$ because it is a bijection, and the same goes for $b=K^K$ . In that case, the sequence converges, and we're done.

At all the other cases, we have the equation $K^p=p^K=C^d=d^C$ , and also we know $K\leq C$ , thus $d\leq p$ .

I admit, I'm kinda stuck here :( . If anyone has an idea how to show that these other solutions are inconsistent, write it in the comments.

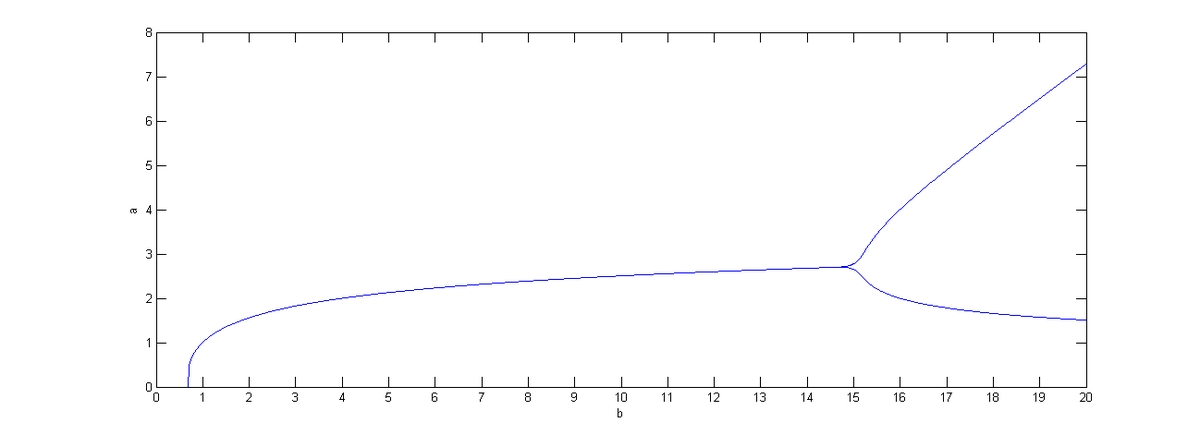
I approached it numerically for positive values of $b$ , I haven't done any math on it (sorry about that) yet I found something funny happening, the series seems to converge to zero for values of $b<B_1\approx 0.6$ , then for values $B_1<b<B_2\approx 15$ it converges to a positive number $a$ (including $a=2$ when $b=4$ ) and then after $B_2$ it stays oscillating in a cycle between two numbers. 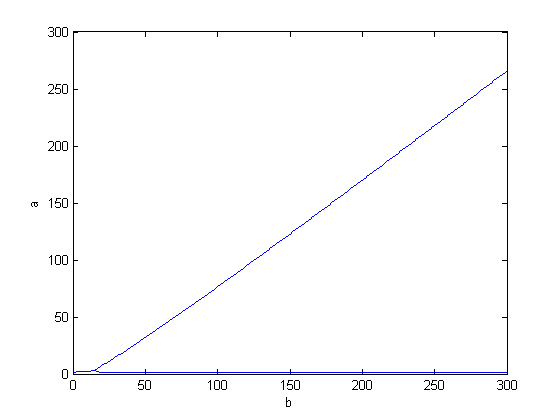Here is what I mean in a picture, for each value of $b$ I'm plotting $a_n$ for $n=990,991,\dots,1000$ : This really reminds me of the behavior of the logistic map, so I plotted for bigger values of $b$ hopping to find something, but the arms just continued without bifurcation apparently in a straight line, here is a picture:

So what I did is i rewrote the sequence as $a_n = b^{b^{-b^{-b^{...{^-1}}}}} (n+1 \text{ copies of b})$

Now i substituted $c=-b$ and took $log_{-c}$ twice: $log_{-c}(log_{-c}(a_n))=c^{c^{c^{c^{...{^-1}}}}} (n-1 \text{ copies of c})$ In order for $a_n$ to converge to a number, the right term must also converge to a number. Now I got stuck here but I'm pretty sure that converges for every $c<0$ or $b>0$ ...

It is clearly a strictly decreasing sequence with terms greater than 1 this as it grows smaller and smaller where would it go