This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
not a question, just the solutions @kritarth lohomi
Nice and simple, just what I did.
Simply, here is from Koro-sensei, kukukuku
x 1 = 2 x 1 = 4 x 1 = 1 6 1 = 1 6 x x = 1 6 1
Follow you? For this piece of nut? Hahaha. No. Btw, just square both sides twice. So simple! I mean, 84% of the people got it right! Whoa.
Square both sides twice..
1/x = 16
x = 1/16
Squaring both sides twice gives x 1 = 1 6 .
Then, solving for x gives us the answer of 1 6 1 .
Simply after squaring both sides twice we get 1/x = 16
X= 1/16 :))
[(1/x)^1/2]^1/2 = 2, Then (1/x)^1/4 = 2; x^-1/4 = 2 ; x^-1 = 2^4 ; 1/x = 2^4 Therefore 1/x = 16, Hence x = 1/16
It is not good to use guess and check for these types of questions. For a start, how did you come up with the number 1/16 and how can you make sure there is only one solution?
Log in to reply
I dont think that is a good solution either.. Trial is okay if you are using numerical approximation. Even for numerical approximation, you have to state your rationale
Where did you come up with the "if x=1/16" ? You knew the answer before you decided what x equals?
Logic: only answer it COULD be: had to be an even number
0.0625 is not an even number
Square both sides to remove the first square root. The equation should now be sqrt(1/x) = 4. Square both sides again, you have 1/x =16. Divide by 16 and multiply by x to make x = 1/16
1/x = y -> substitute 1/x for y
√√y = 2 y = 2^4 y = 16 -> 1/x must be 16 to satisfy the condition
1/x = 16 16x = 1 x = 1/16 -> for 1/x be 16, x must be 1/16
answer = 1/16
((x^{-1})^{1/2})^{1/2}=2
x^{-1/4}=2
(x^{-1/4})^{-4}=2^{-4}
x=1/2^{4}=1/16
In This Case, You have To Keep Breaking The Square Root And That Means Starting From The Inside Of The Square Root And Work your Way Onto The Outer Square Root To Get 2
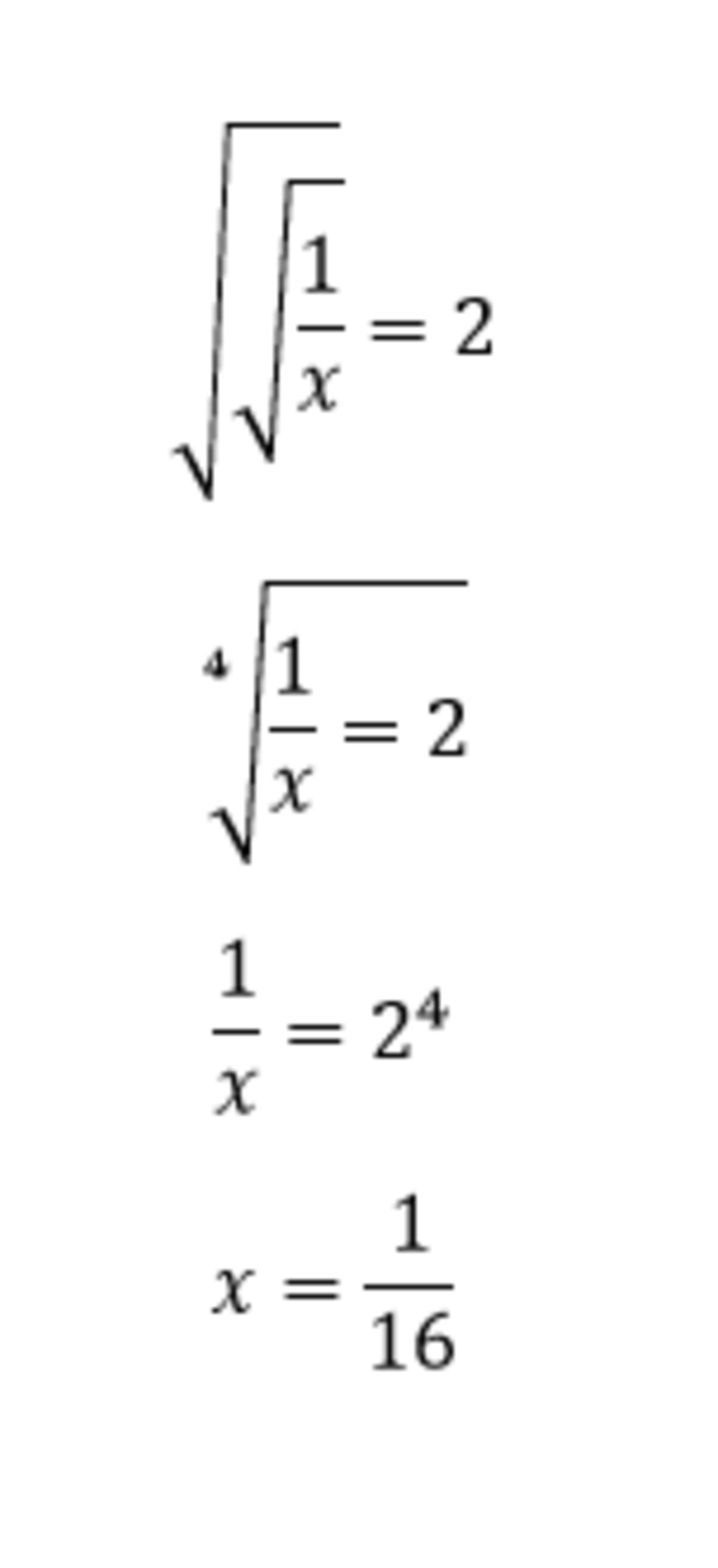
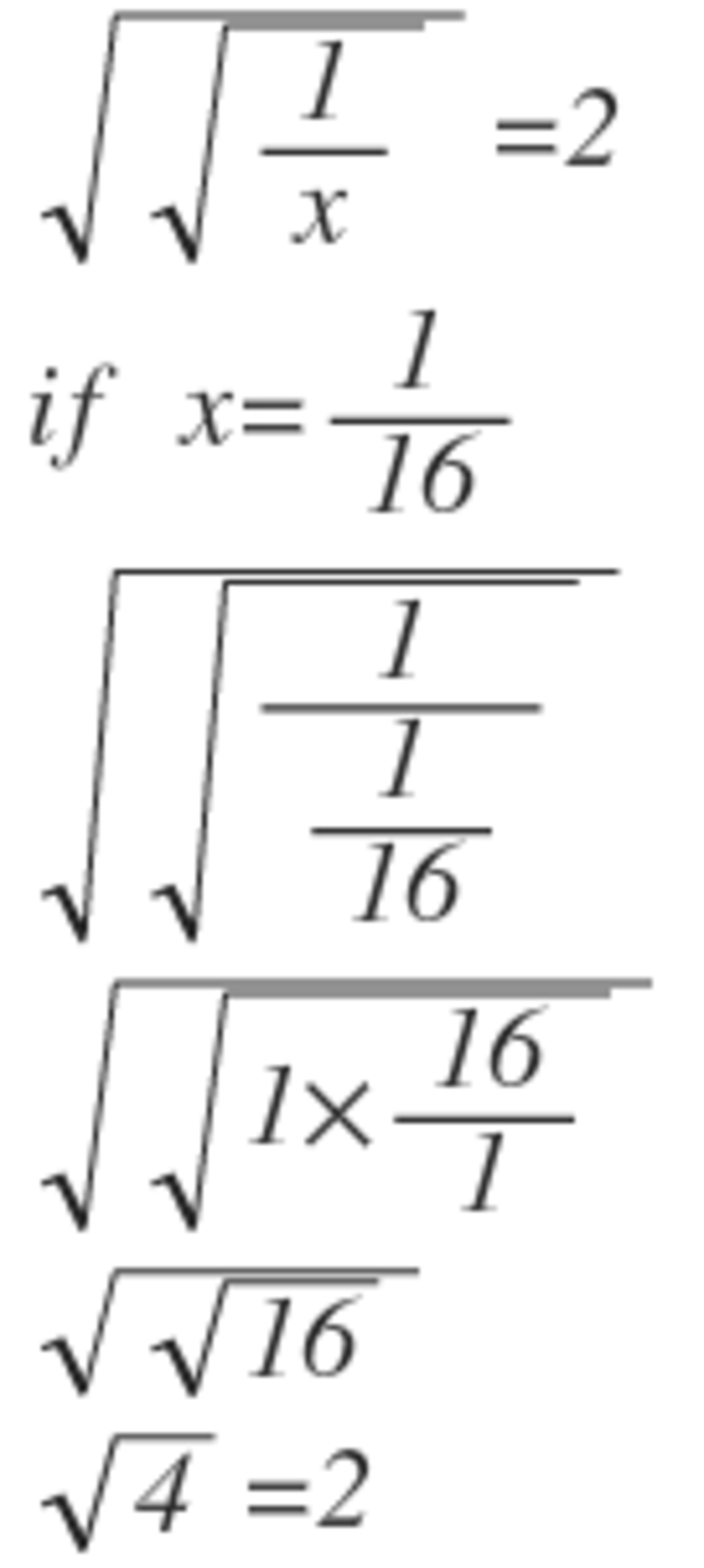
Square both sides of the original equation to obtain:
x 1 = 4 .
Then square both sides again:
x 1 = 1 6 ⟶ x = 1 6 1