Nested Quantum Wells
A particle in a one-dimensional quantum well is governed by a variant of the time-independent Schrodinger equation, expressed in terms of wave function Ψ ( x ) .
The quantities V and E are the potential energy and total energy, respectively. E is a positive constant.
− d x 2 d 2 Ψ ( x ) + V ( x ) Ψ ( x ) = E Ψ ( x )
The potential energy varies as follows:
V ( x ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ∞ , 0 , 1 0 0 , 0 , 1 0 0 , 0 , ∞ , x < − 1 − 1 ≤ x < − 0 . 2 − 0 . 2 ≤ x < − 0 . 1 − 0 . 1 ≤ x < + 0 . 1 + 0 . 1 ≤ x < + 0 . 2 + 0 . 2 ≤ x ≤ + 1 x > + 1
The boundary conditions on Ψ ( x ) are:
Ψ ( x ) = { 0 , x ≤ − 1 0 , x ≥ + 1
For the smallest allowable E such that E > 0 , what is the probability of detecting the particle within the range − 0 . 1 ≤ x ≤ + 0 . 1 ?
Note: You will likely need a computer to solve this. The image below shows a plot of Ψ 2 ( x ) vs. x , with the V = 0 regions shaded. Ψ ( x ) is not normalized in the plot.
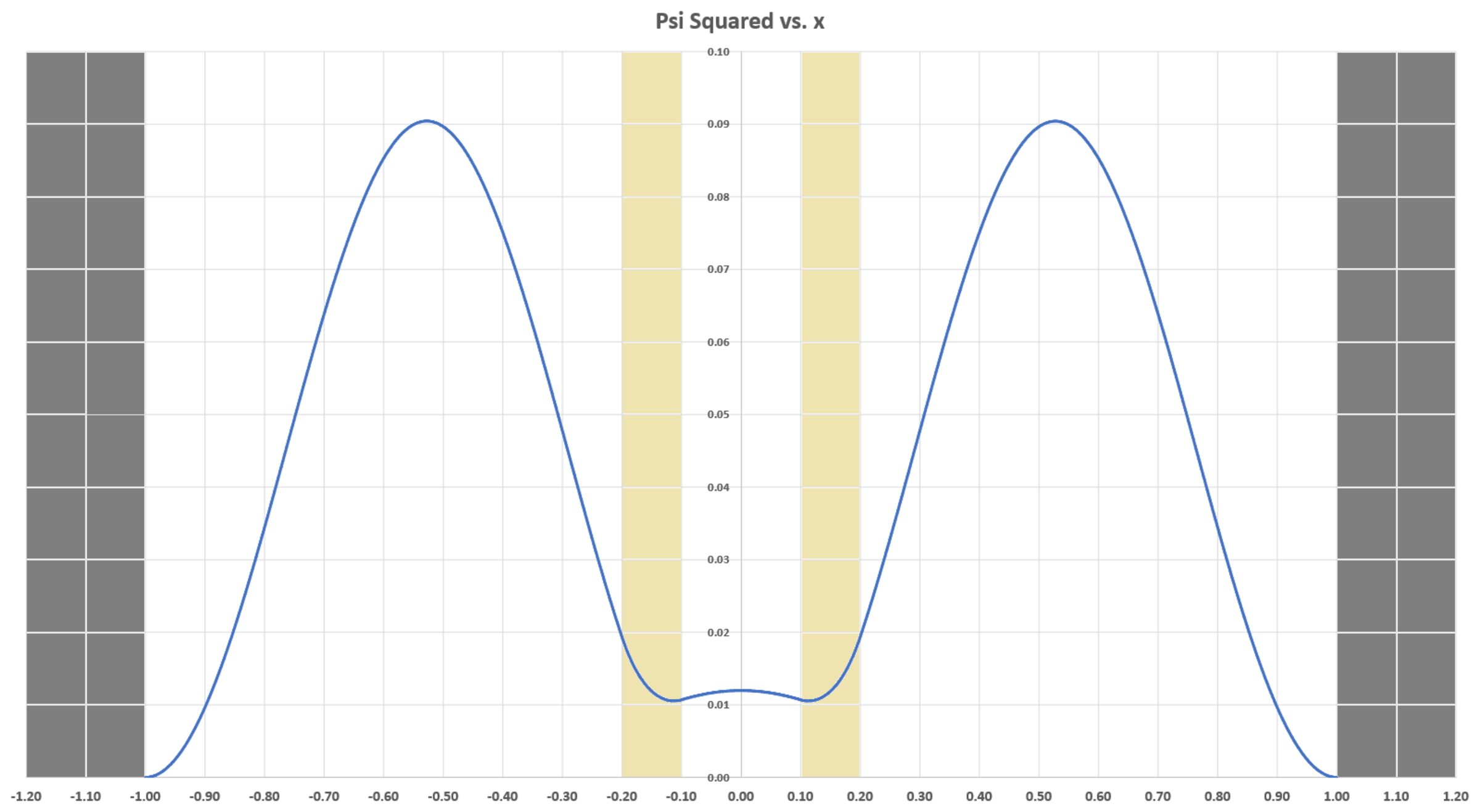
The answer is 0.0261.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Really nice! Your solutions always make me reflect on the shortcuts that I almost never hesitate to take.
See the solution by @Karan Chatrath for details. Basically, sweep the energy E over a range, and make a plot of Ψ ( + 1 ) vs. E , assuming that Ψ ( − 1 ) = 0 and d x d Ψ ( − 1 ) = 1 . The allowable values of E are those for which Ψ ( 1 ) = 0 .
Intuitively, I want to see that the particle spends "little time" in the middle, because of the potential well there. With E 1 (the first allowable value of E ), that is indeed the case. But plotting Ψ 2 ( x ) for various E values reveals that the odd-subscript modes (ex: ( 1 , 3 , 5 ) ) are tolerant of the center region to some extent, while the even-subscript modes are not. I suppose this makes sense, since the number of "humps" in the plot of Ψ 2 ( x ) is equal to the mode number. For odd modes, symmetry of the plot requires that there be a central hump, with equal numbers of humps on either side. Even modes naturally omit the central hump as a result of symmetry. You can see that mode 1 is sort of an exception to this even/odd rule, likely because the inner potential barriers are large relative to the system energy. For large E , the inner potential barrier is less important, and the wave function obeys the even/odd hump rule very regularly.
The plots of Ψ 2 ( x ) for E 2 through E 7 are shown below.
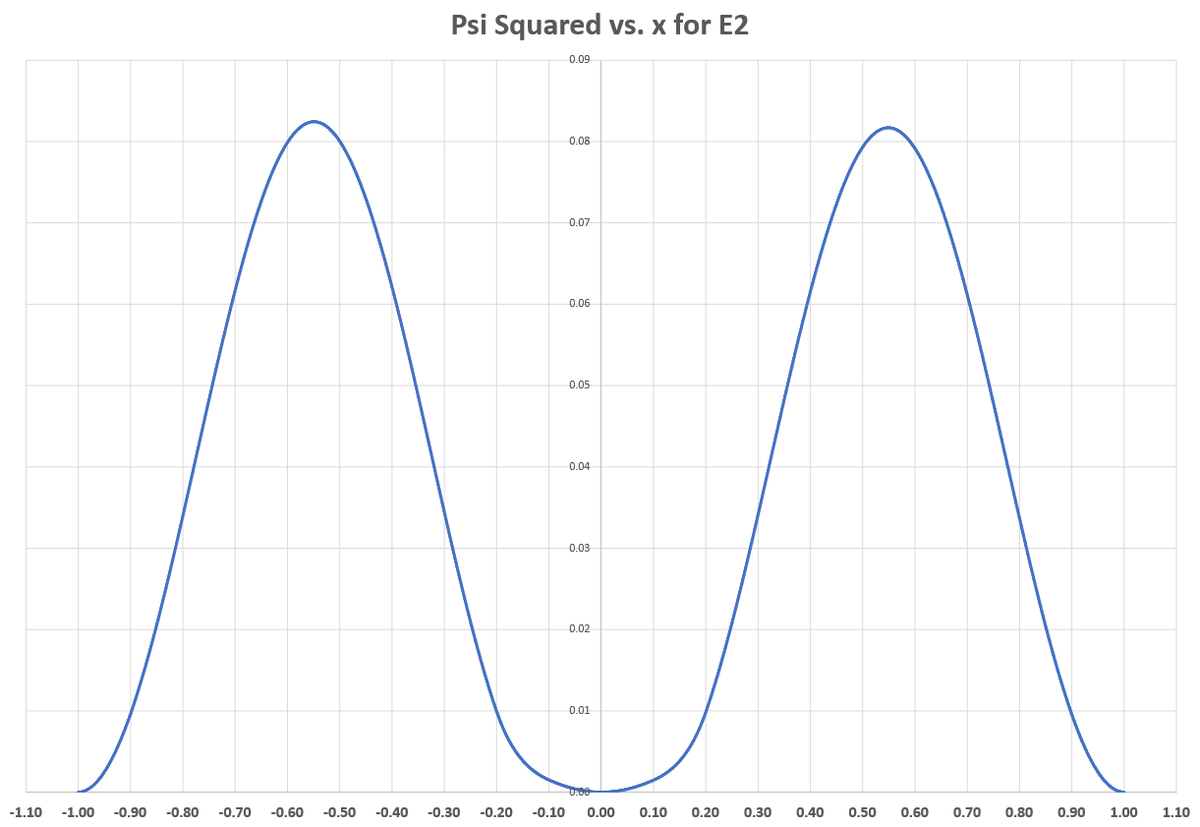
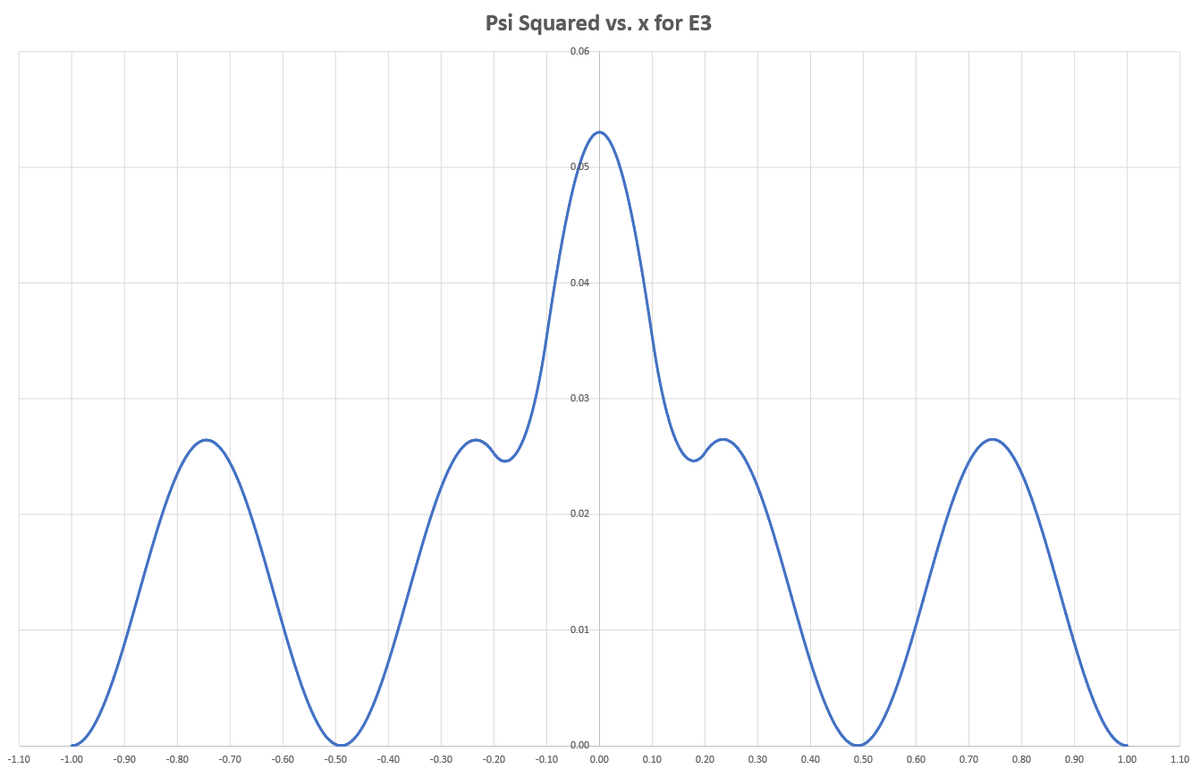
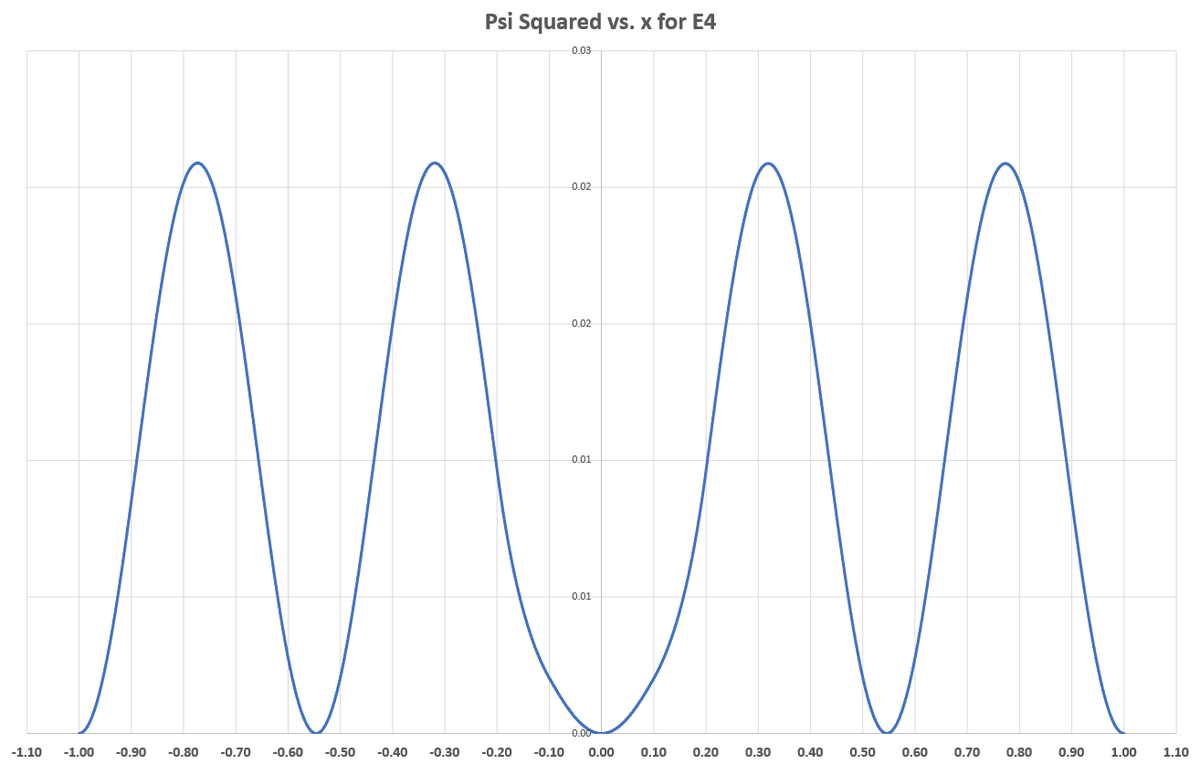
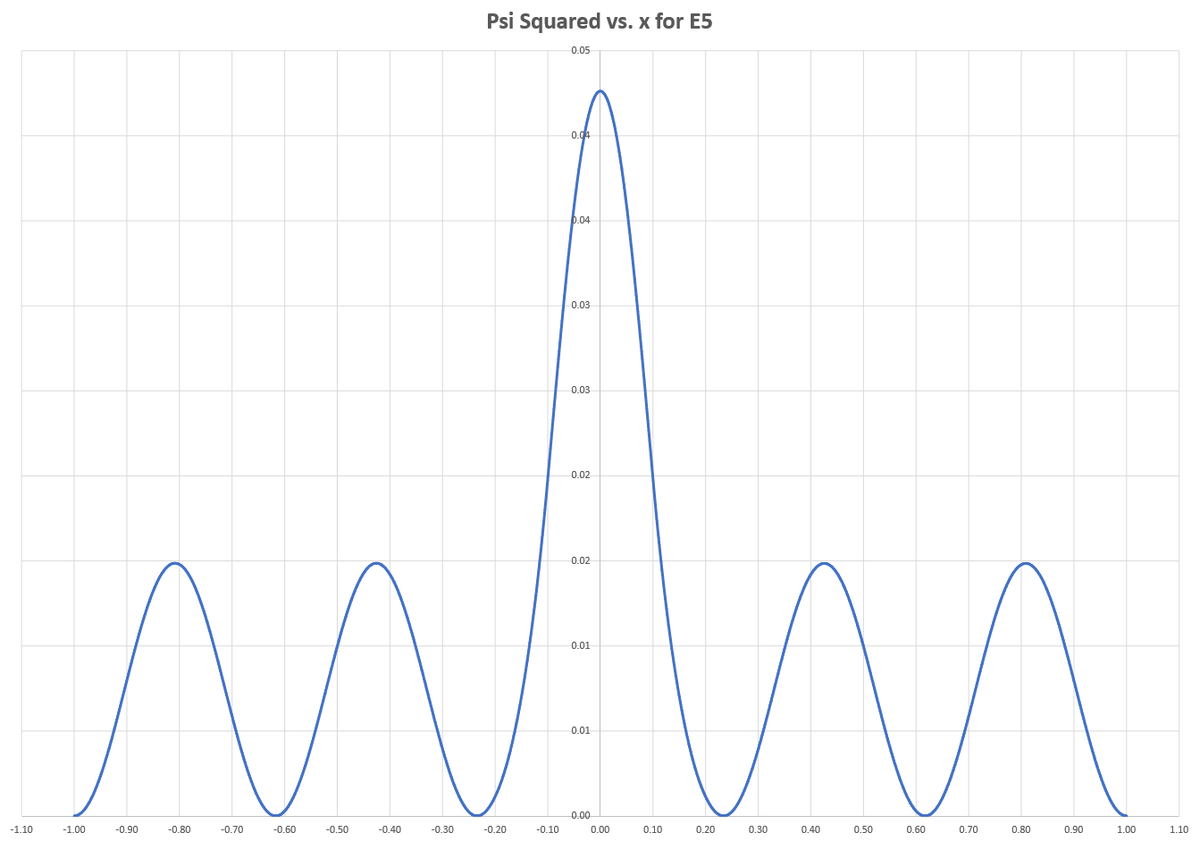
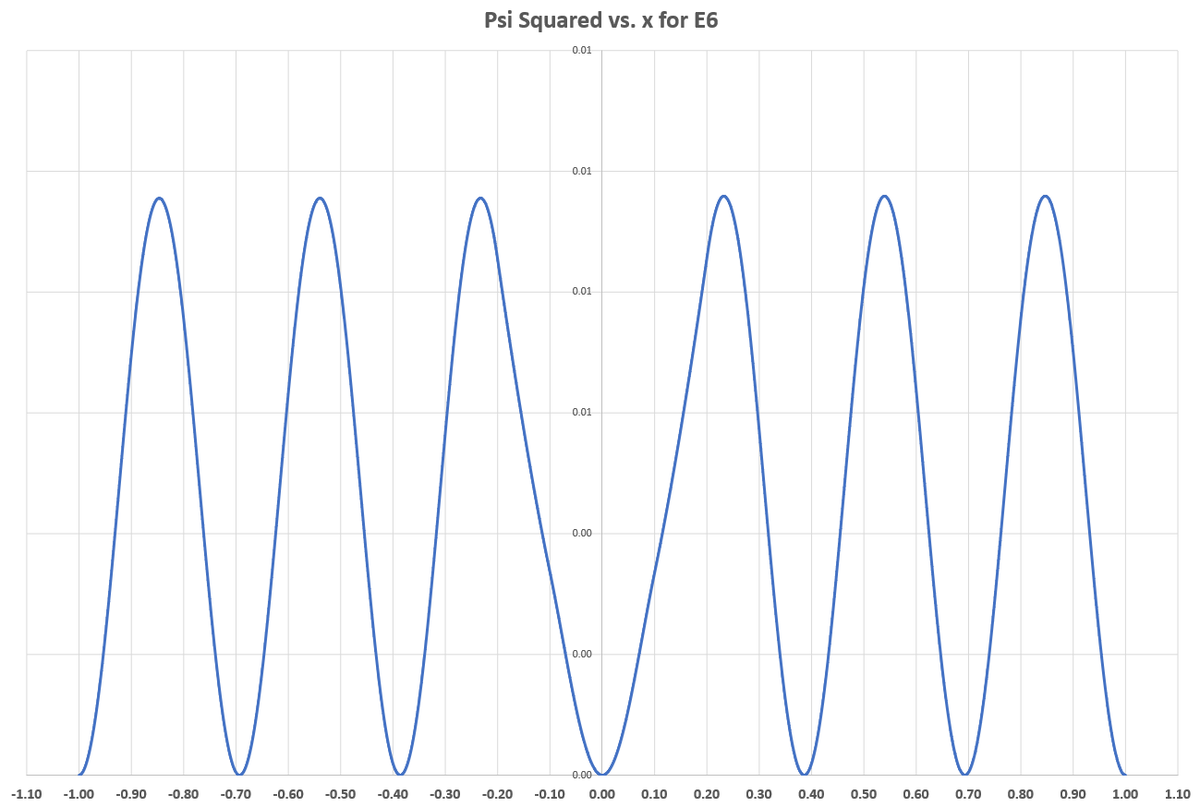
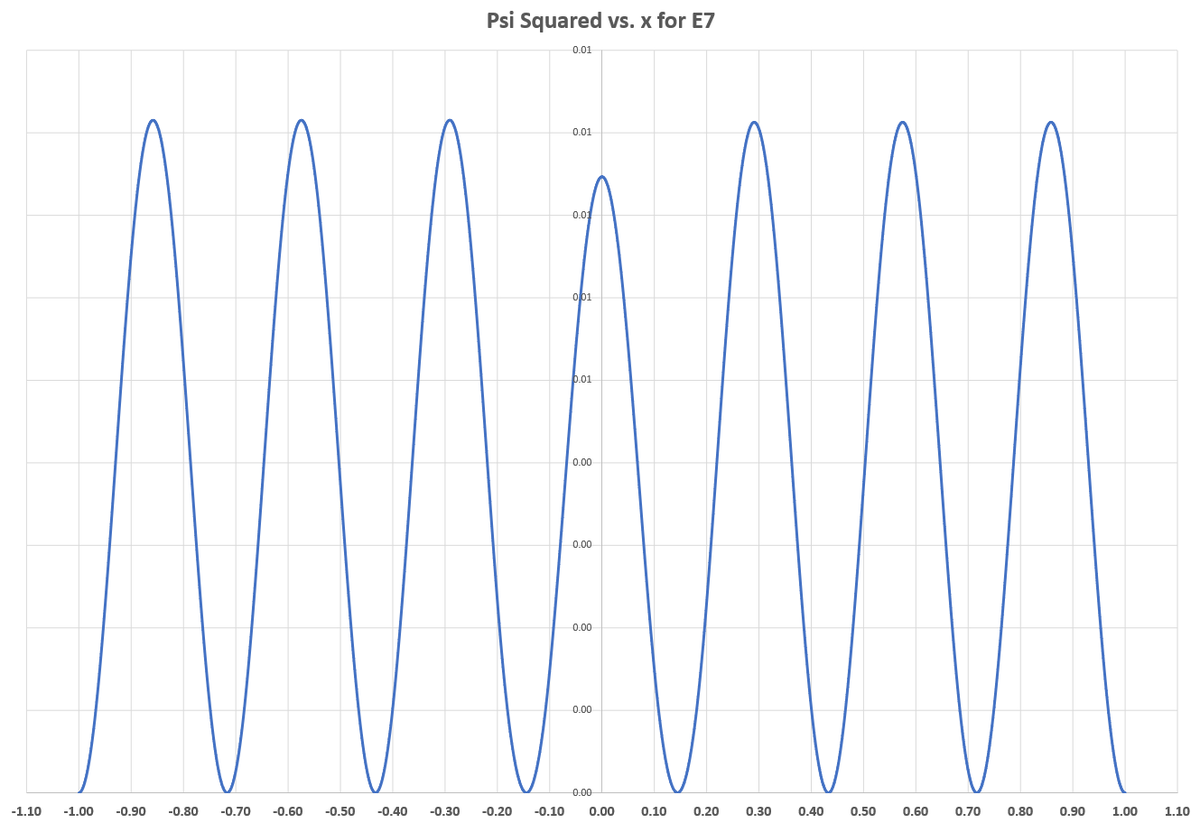
@Steven Chase nice drawing and art.upvoted :)
The calculations are done using a computer. This problem is interesting cause its result is in agreement with classical thought which is that a particle always moves towards its region of minimum potential energy. Analogous to that, in this case, the particle is more likely to be found in area of lower potential.
The code attached below is commented. Lines starting with '%' are comments, which the reader is requested to focus on.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
|
The Hamiltonian of this system commutes with the parity operator ( P Ψ ) ( x ) = Ψ ( − x ) , and hence energy levels will be associated with either even or odd wave functions. Assuming that 0 < E < 1 0 0 , we write E = k 2 and κ = 1 0 0 − k 2 , so that the wave equation is Ψ ′ ′ ( x ) + k 2 Φ ( x ) = 0 for ∣ x ∣ < 0 . 1 and 0 . 2 < ∣ x ∣ < 1 , while the wave equation is Ψ ′ ′ ( x ) − κ 2 Ψ ( x ) = 0 for 0 . 1 < ∣ x ∣ < 0 . 2 . Moreover Ψ ( x ) = 0 for ∣ x ∣ > 1 .
Looking for even wave functions, we want Ψ S of the form
Ψ S ( x ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ sin k ( x − 1 ) A cosh κ x + B sinh κ x C cos k x Ψ S ( − x ) 0 . 2 < x < 1 0 . 1 < x < 0 . 2 0 < x < 0 . 1 − 1 < x < 0
and since Ψ S and Ψ S ′ must be continuous for 0 < x < 1 , we can use the conditions at 0 . 2 to find A , B in terms of k , κ . The conditions at 0 . 1 then give two different expressions for C in terms of k , κ . For a valid energy level we need these expressions to be the same. This gives the equation κ tan ( 5 4 k ) + k tanh ( 5 1 κ ) k + κ tan ( 5 4 k ) tanh ( 5 1 κ ) = κ cot ( 1 0 1 k ) + k tanh ( 1 0 1 κ ) k + κ cot ( 1 0 1 k ) tanh ( ! 0 1 κ )
Solving this equation numerically, we find valid even solutions for k = 3 . 3 2 5 5 6 , 6 . 1 5 2 5 8 , 8 . 2 0 4 .
Looking for odd wave functions, we want Ψ A of the form
Ψ A ( x ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ sin k ( x − 1 ) A cosh κ x + B sinh κ x C sin k x − Ψ A ( − x ) 0 . 2 < x < 1 0 . 1 < x < 0 . 2 0 < x < 0 . 1 − 1 < x < 0 and the same continuity considerations lead us to the equation κ tan ( 5 4 k ) + k tanh ( 5 1 κ ) k + κ tan ( 5 4 k ) tanh ( 5 1 κ ) + κ tan ( 1 0 1 k ) − k tanh ( 1 0 1 κ ) k − κ tan ( ! 0 1 k ) tanh ( 1 0 1 κ ) = 0 which solves to give valid odd solutions for k = 3 . 4 8 3 6 5 , 6 . 9 2 0 0 6 .
Thus the smallest permissible energy level is given by k = 3 . 3 2 5 5 6 , and so the smallest energy level is E = 1 1 . 0 5 9 3 , and the wave function is even. The desired probability is ∫ R ∣ ∣ Ψ S ( x ) ∣ ∣ 2 d x ∫ − 0 . 1 0 . 1 ∣ ∣ Ψ S ( x ) ∣ ∣ 2 d x = 0 . 0 2 6 1 0 0 3
For energy levels beyond the first five, E > 1 0 0 and so the shape of the wave function changes from A cosh κ x + B sinh κ x to A cos λ x + B sin λ x where λ = E 2 − 1 0 0 . This explains the increasingly sinusoidal shape of the wave functions in @Steven Chase 's solution. Also note that, as is normal in these problems, the odd and even energy levels alternate, which correponds to Steven's observation about the regularity of the even/odd hump pattern (even wave functions have a hump at the origin, while odd wave functions vanish at the origin).