Yet Another Nested Radicals
4
+
1
0
4
+
1
2
4
+
1
4
⋯
Find the value of this expression.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
well, no offence but i really think maths problems should be based on solving using logic rather than some already found formula. You see, I have failed to do this question without the formula and I think, directly applying the formula does not give anybody a good challenge. again, no offence
Log in to reply
Its just like disliking english just because your vocabulary is weak.... no offence.....
it's like fingers is to man in the same way, formula is to mathematics... you always use formulas ranging form ( a + b ) 2 to even the very complex ones... just because you don't know the derivation of a formula doesn't mean you can't use it or even hate it... using it is great!! thanks to Ramanujan for this great formula... people who agree may upvote!!!
nice i like it
May i get a proof of it ?.
Log in to reply
Here is the proof f ( x ) = x + n = [ x + n ] 2 = n 2 + x ( x + n + n ) = n 2 + x f ( x + n ) . And this is repeated...
nice solution.... :)
By logic....1st root from start.....4 added to multiple of 10 can't yield odd.....Therefore ans must be even....now 10 or 12 ...can't be 10 as under root it can't be 100...The no. In root will have unit digit 4 as 4 added to multiple of 10....Hence 12
I didnt know the formula so i just observed that if you followed the pattern in the opposite way and took off the square root you could get the answer.
Can you explain your solution?
Ramanujan 's formula
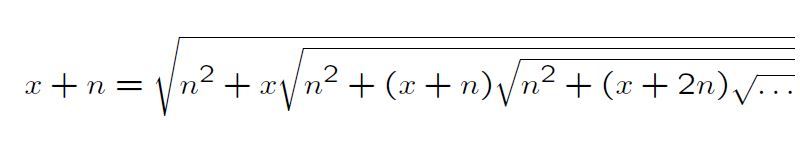
as seen in image
putting x=10 and n=2 ,
=x+n
=10+2
= 12