Nested Radicals........

Algebra Level 2

$\large 2^{\sqrt{2^{\sqrt{2^{\sqrt{2^{\ldots}}}}}}} = \ ?$

4

\sqrt 2

1

2

5 solutions

Niaz Ghumro
Mar 3, 2015

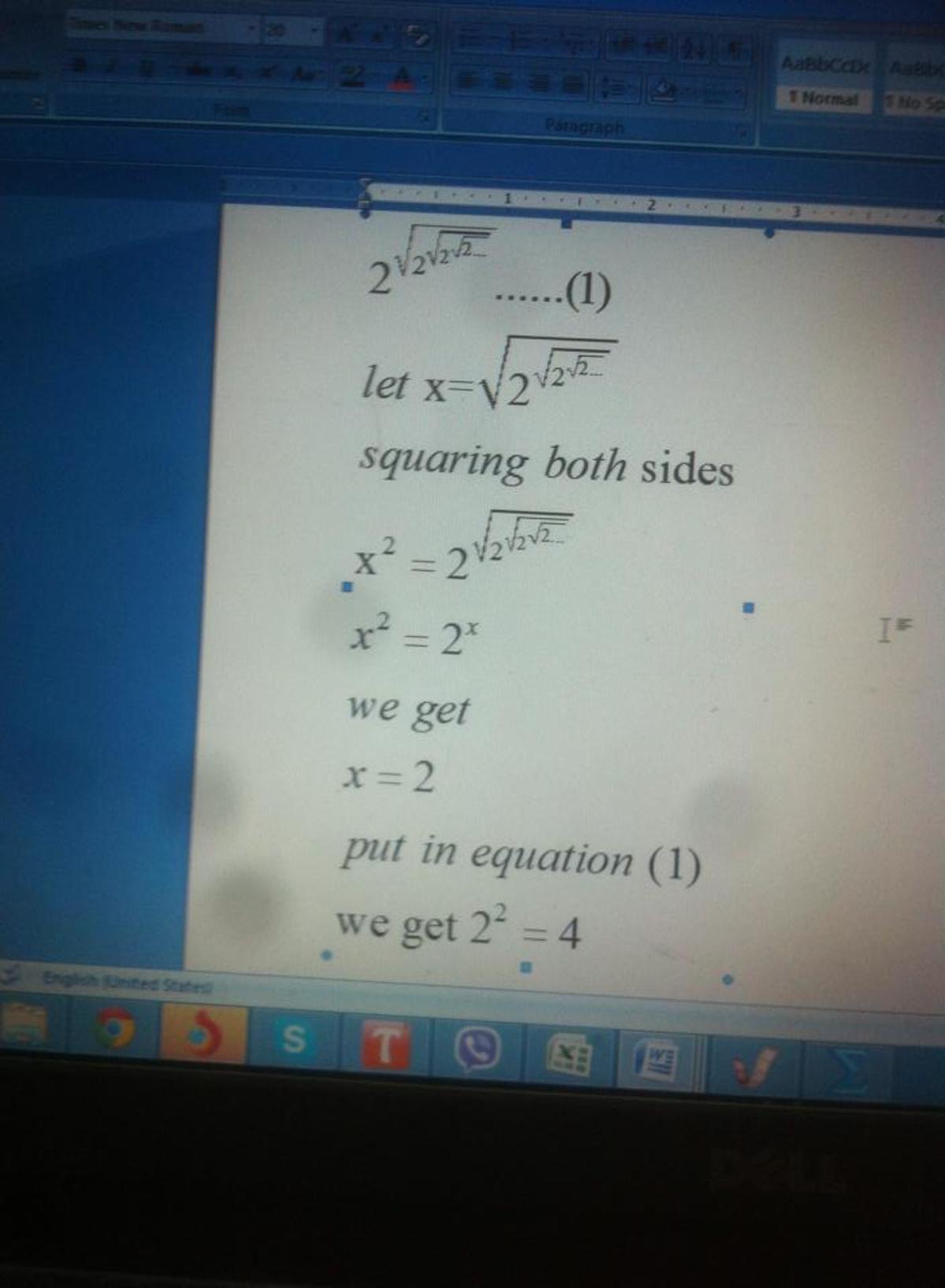
$x=4$ also solves $x^2=2^x$ .

Akiva Weinberger - 6 years, 1 month ago

Curtis Clement
Feb 19, 2015

$\sqrt{2} = 2^{\dfrac{1}{2}}$ so by canceling the expression becomes $2^2 = 4$

Aaaaa Bbbbb
Feb 17, 2015

$\sqrt{2^{\sqrt{2^{...}}}}=A$ $\Rightarrow A^2=2^A$ $A=\boxed{4}$

$A != 4, A = 2$ , and according to the question it will be ${A}^{2} = 4$ (the answer. But I couldn't get why $A =2$ and not $4$

Kartik Sharma - 6 years, 3 months ago

I think he has made a typo - the whole expression should be 4 not A. Really, A = 2 and $A^{2}$ = $2^{A}$ = 4.

Curtis Clement - 6 years, 3 months ago

By that logic, the answer should be 16. However, the expression does not approach that value.

Blan Morrison - 2 years, 7 months ago

Rafael Fedora Rafael Fedor
Mar 14, 2015

X^2=(√2*√2)^x. So x^2=2^× and there. Is. Only one solution. X=4. Rafael Trevor ':

but why not X=2

Sai Sameera Bunni - 5 years, 10 months ago

Jonathan Alvaro
Jan 12, 2016

The simplest solution would be : Square root of 2 is approximately 1.4

Which means that the answer is bigger than 2 thus leaving only 4