Nested Radicals

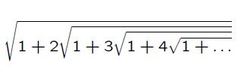
Let's start with forming a nested radical expression for $x$ : $|x|=\sqrt{x^2}\\=\sqrt{1+(x-1)(x+1)}\\=\sqrt{1+(x-1)\sqrt{1+x(x+2)}}\\=\sqrt{1+(x-1)\sqrt{1+x\sqrt{1+(x+1)(x+3)}}}$ In the same way if we continue indefinitely,we get the following nested radical expression for $x$ : $|x|=\sqrt{1+(x-1)\sqrt{1+x\sqrt{1+(x+1)\sqrt{1+(x+2)\sqrt{1+(x+3)\sqrt{\cdots}}}}}}$ By observation this expression fits the form of the question,so simply put $x=3$ to get: $\boxed{3=\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{\cdots}}}}}$

Ramanujan 's formula

as seen in image
putting x=2 and n=1 ,
=x+n
=2+1
= 3

Let f(x) be $\sqrt { 1+x\sqrt { 1+(x+1)\sqrt { 1+......... } } }$ .Note that ${ f\left( x \right) }^{ 2 }=x*f(x+1)\quad +\quad 1$ . Through observation, f(x)=x+1. Question is nothing else but f(2) i.e 2+1=3