Nested Regular n-gons and Spheres 2

Probability Level 3

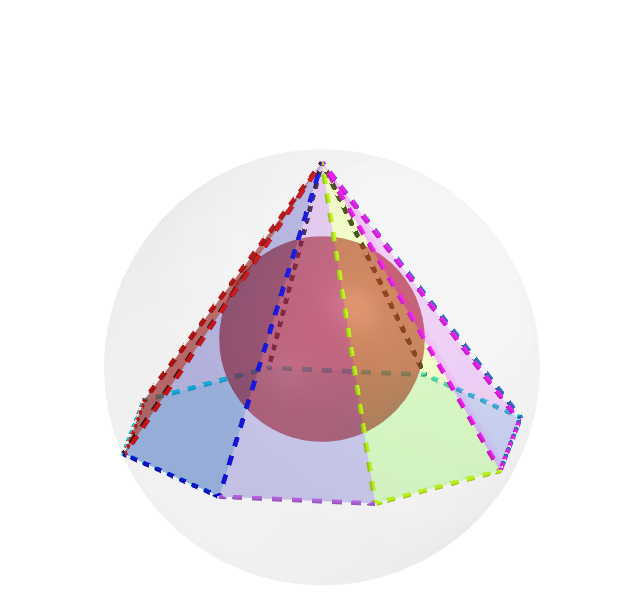
Let n ≥ 4 n \geq 4 be a fixed positive integer.

For each positive integer m m ,

Let V p ( m ) V_{p}(m) be the volume of the largest n n -gonal pyramid inscribed in a sphere of volume V s ( m ) V_{s}(m)

and

Let V s ( m + 1 ) V_{s}(m + 1) be the volume of the largest sphere inscribed in the n n -gonal pyramid of volume V p ( m ) V_{p}(m) which is tangent to the faces of the n n -gonal pyramid.

Let V s ( n ) = ∑ m = 1 ∞ V s ( m ) V_{s}(n) = \sum_{m = 1}^{\infty} V_{s}(m) and V p ( n ) = ∑ m = 1 ∞ V p ( m ) V_{p}(n) = \sum_{m = 1}^{\infty} V_{p}(m) and P ( n ) = V s ( n ) ∗ V p ( n ) V s ( 1 ) 2 P(n) =\dfrac{V_{s}(n) * V_{p}(n)}{V_{s}(1)^2}

If A = lim ⁡ n → ∞ P ( n ) A = \lim_{n \rightarrow \infty} P(n) can be expressed as A = ( a b ) b ( ( b α ) b ( b α ) b − a b ) a A = (\dfrac{a}{b})^b(\dfrac{(b\alpha)^b}{(b\alpha)^b - a^b})^a , where α = c + b a \alpha = \dfrac{c + \sqrt{b}}{a} and a , b a,b and c c are coprime positive integers, find a + b + c a + b + c .

Note: It may be difficult to obtain the form above and find α \alpha , but it can be done. Of course you could obtain the same result by reducing the problem to Nested Cones and Spheres, but that was not my intention. My intention was to use the n n -gonal pyramids for fixed n n and then evaluate lim ⁡ n → ∞ P ( n ) \lim_{n \rightarrow \infty} P(n) and obtain the above form.


The answer is 6.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jan 24, 2019

V s ( 1 ) = 4 3 π R 1 3 V_{s}(1) =\dfrac{4}{3}\pi R_{1}^3 .

x = 2 r 1 sin ⁡ ( π n ) x = 2r_{1}\sin(\dfrac{\pi}{n}) and h = r 1 cos ⁡ ( π n ) ⟹ A △ A B C = n 2 sin ⁡ ( 2 π n ) r 1 2 ⟹ V 1 ( p ) = n 6 sin ⁡ ( 2 π n ) r 1 2 H 1 h = r_{1}\cos(\dfrac{\pi}{n}) \implies A_{\triangle_{ABC}} = \dfrac{n}{2}\sin(\dfrac{2\pi}{n})r_{1}^2 \implies V_{1}(p) = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})r_{1}^2H_{1}

R 1 2 = ( H 1 − R 1 ) 2 + r 1 2 ⟹ r 1 2 = 2 H 1 R 1 − H 1 2 ⟹ V 1 = n 6 sin ⁡ ( 2 π n ) ( 2 H 1 2 R 1 − H 1 3 ) ⟹ R_{1}^2 = (H_{1} - R_{1})^2 + r_{1}^2 \implies r_{1}^2 = 2H_{1}R_{1} - H_{1}^2 \implies V_{1} = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})(2H_{1}^2R_{1} - H_{1}^3) \implies d V 1 ( p ) d H 1 = n 6 sin ⁡ ( 2 π n ) H 1 ( 4 R 1 − 3 H 1 ) = 0 ⟹ H 1 = 4 R 1 3 ⟹ r 1 = 2 2 3 R 1 \dfrac{dV_{1}(p)}{dH_{1}} = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})H_{1}(4R_{1} - 3H_{1}) = 0 \implies H_{1} = \dfrac{4R_{1}}{3} \implies r_{1} = \dfrac{2\sqrt{2}}{3}R_{1}

s = h 2 + H 1 2 = 2 2 3 cos ⁡ 2 ( π n ) + 2 R 1 s = \sqrt{h^2 + H_{1}^2} = \dfrac{2\sqrt{2}}{3}\sqrt{\cos^2(\dfrac{\pi}{n}) + 2}R_{1}

The area of the above triangle is A = h H 1 = ( h + s ) R 2 ⟹ R 2 = h H 1 h + s A = hH_{1} = (h + s)R_{2} \implies R_{2} = \dfrac{hH_{1}}{h + s}

h H 1 = 8 2 9 cos ⁡ ( π n ) R 1 2 hH_{1} = \dfrac{8\sqrt{2}}{9}\cos(\dfrac{\pi}{n})R_{1}^2 and h + s = 2 2 3 ( cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 ) R 1 ⟹ h + s = \dfrac{2\sqrt{2}}{3}(\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2})R_{1} \implies R 2 = 4 cos ⁡ ( π n ) R 1 3 ( cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 ) R_{2} = \dfrac{4\cos(\dfrac{\pi}{n})R_{1}}{3(\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2})}

Let a n = cos ⁡ ( π n ) cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 = a_{n} = \dfrac{\cos(\dfrac{\pi}{n})}{\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2}} = 1 1 + 1 + 2 sec ⁡ 2 ( π n ) \dfrac{1}{1 + \sqrt{1 + 2\sec^2(\dfrac{\pi}{n})}}

Now let ϕ ( n ) = 1 + 1 + 2 sec ⁡ 2 ( π n ) 2 ⟹ j ( n ) = 4 3 a n = 2 3 ϕ ( n ) ⟹ R 2 = j ( n ) R 1 = 2 3 ϕ ( n ) R 1 \phi(n) = \dfrac{1 + \sqrt{1 + 2\sec^2(\dfrac{\pi}{n})}}{2} \implies j(n) = \dfrac{4}{3}a_{n} = \dfrac{2}{3\phi(n)} \implies R_{2} = j(n)R_{1} = \dfrac{2}{3\phi(n)}R_{1}

and ⟹ r 2 = 2 2 3 R 2 = 2 2 3 ( 2 3 ϕ ( n ) ) R 1 \implies r_{2} = \dfrac{2\sqrt{2}}{3}R_{2} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})R_{1} , H 2 = 4 3 R 2 = 4 3 ( 2 3 ϕ ( n ) ) R 1 , \:\ H_{2} = \dfrac{4}{3}R_{2} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})R_{1}, R 3 = 2 3 ϕ ( n ) R 2 = ( 2 3 ϕ ( n ) ) 2 R 1 , \:\ R_{3} = \dfrac{2}{3\phi(n)}R_{2} = (\dfrac{2}{3\phi(n)})^2R_{1}, r 3 = 2 2 3 R 3 = 2 2 3 ( 2 3 ϕ ( n ) ) 2 R 1 , \:\ r_{3} = \dfrac{2\sqrt{2}}{3}R_{3} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})^2R_{1}, H 3 = 4 3 R 3 = 4 3 ( 2 3 ϕ ( n ) ) 2 R 1 \:\ H_{3} = \dfrac{4}{3}R_{3} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})^2R_{1}

In General:

R m = ( 2 3 ϕ ( n ) ) m − 1 R 1 R_{m} = (\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

r m = 2 2 3 ( 2 3 ϕ ( n ) ) m − 1 R 1 r_{m} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

h m = 4 3 ( 2 3 ϕ ( n ) ) m − 1 R 1 h_{m} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

⟹ V s ( m ) = ( 8 27 ϕ ( n ) ) m − 1 V s ( 1 ) \implies V_{s}(m) = (\dfrac{8}{27\phi(n)})^{m - 1}V_{s}(1) and V p ( m ) = 4 27 π n sin ⁡ ( 2 π n ) ( 8 27 ϕ ( n ) ) m − 1 V s ( 1 ) V_{p}(m) = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{8}{27\phi(n)})^{m - 1}V_{s}(1)

⟹ \implies

V s ( n ) = V s ( 1 ) ∑ m = 1 ∞ ( 8 27 ϕ ( n ) ) m − 1 = 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 V s ( 1 ) V_{s}(n) = V_{s}(1)\sum_{m = 1}^{\infty} (\dfrac{8}{27\phi(n)})^{m - 1} = \dfrac{27\phi^3(n)}{27\phi^3(n) - 8}V_{s}(1)

and

V p ( n ) = 4 27 π n sin ⁡ ( 2 π n ) ( 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 ) V s ( 1 ) V_{p}(n) = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{27\phi^3(n)}{27\phi^3(n) - 8})V_{s}(1)

⟹ V s ( n ) ∗ V p ( n ) V s ( 1 ) 2 = 4 27 π n sin ⁡ ( 2 π n ) ( 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 ) 2 \implies \dfrac{V_{s}(n) * V_{p}(n)}{V_{s}(1)^2} = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{27\phi^3(n)}{27\phi^3(n) - 8})^2

For nested cones and spheres we have: α = lim ⁡ n → ∞ ϕ ( n ) = 1 + 3 2 \alpha = \lim_{n \rightarrow \infty} \phi(n) = \dfrac{1 + \sqrt{3}}{2} and lim ⁡ n → ∞ n sin ⁡ ( 2 π n ) = 2 π \lim _{n \rightarrow \infty} n\sin(\dfrac{2\pi}{n}) = 2\pi .

Letting P ( n ) = V s ( n ) ∗ V p ( n ) V s ( 1 ) 2 ⟹ A = lim ⁡ n → ∞ P ( n ) = 8 27 ( 27 α 3 27 α 3 − 8 ) 2 = ( 2 3 ) 3 ( ( 3 α ) 3 ( 3 α ) 3 − 2 3 ) 2 = ( a b ) b ( ( b α ) b ( b α ) b − a b ) a P(n) = \dfrac{V_{s}(n) * V_{p}(n)}{V_{s}(1)^2} \implies A = \lim_{n \rightarrow \infty} P(n) = \dfrac{8}{27}(\dfrac{27\alpha^3}{27\alpha^3 - 8})^2 = (\dfrac{2}{3})^3(\dfrac{(3\alpha)^3}{(3\alpha)^3 - 2^3})^2 = (\dfrac{a}{b})^b(\dfrac{(b\alpha)^b}{(b\alpha)^b - a^b})^a ⟹ a + b + c = 6 \implies a + b + c = \boxed{6} .

My problem on Nested square pyramids and spheres

My problem on Nested Tetrahedrons and spheres

For Nested square pyramids and spheres ϕ ( 4 ) = 1 + 5 2 \phi(4) = \dfrac{1 + \sqrt{5}}{2} and V s ( 4 ) ∗ V p ( 4 ) V s ( 1 ) 2 = 16 27 π ( 27 ϕ 3 ( 4 ) 27 ϕ 3 ( 4 ) − 8 ) 2 \dfrac{V_{s}(4) * V_{p}(4)}{V_{s}(1)^2} = \dfrac{16}{27\pi}(\dfrac{27\phi^3(4)}{27\phi^3(4) - 8})^2 .

For Nested tetrahedrons and spheres ϕ ( 3 ) = 2 \phi(3) = 2 and V s ( 3 ) ∗ V p ( 3 ) V s ( 1 ) 2 = 3 4 3 2 ∗ 1 3 2 π \dfrac{V_{s}(3) * V_{p}(3)}{V_{s}(1)^2} = \dfrac{3^4\sqrt{3}}{2* 13^2\pi} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...