Nested Regular n-gons and Spheres

Geometry Level 4

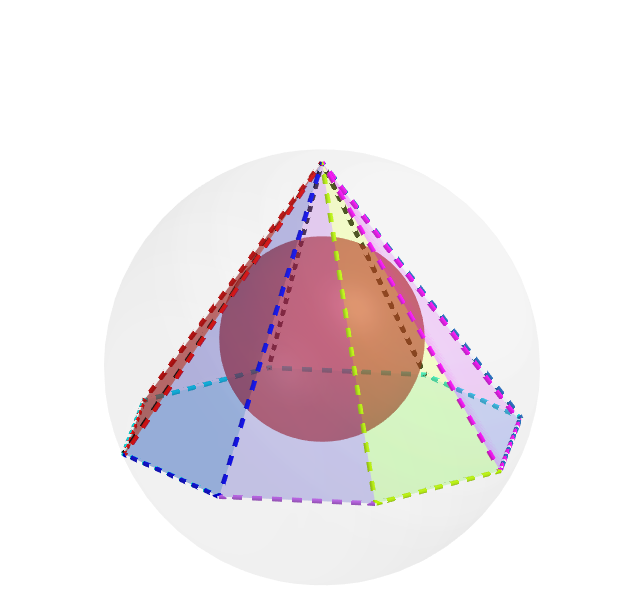
Let n ≥ 4 n \geq 4 be a fixed positive integer.

For each positive integer m m ,

Let V p ( m ) V_{p}(m) be the volume of the largest n n -gonal pyramid inscribed in a sphere of volume V s ( m ) V_{s}(m)

and

Let V s ( m + 1 ) V_{s}(m + 1) be the volume of the largest sphere inscribed in the n n -gonal pyramid of volume V p ( m ) V_{p}(m) which is tangent to the faces of the n n -gonal pyramid.

Let V s = ∑ m = 1 ∞ V s ( m ) V_{s} = \sum_{m = 1}^{\infty} V_{s}(m) and V p = ∑ m = 1 ∞ V p ( m ) V_{p} = \sum_{m = 1}^{\infty} V_{p}(m) and

let ϕ ( n ) = 1 + 1 + 2 sec ⁡ 2 ( π n ) 2 \phi(n) = \dfrac{1 + \sqrt{1 + 2\sec^2(\dfrac{\pi}{n})}}{2} .

If V s ∗ V p V s ( 1 ) 2 = a a b b π n sin ⁡ ( 2 π n ) ( ( b ϕ ( n ) ) b ( b ϕ ( n ) ) b − a b ) a \dfrac{V_{s} * V_{p}}{V_{s}(1)^2} = \dfrac{a^a}{b^b\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{(b\phi(n))^b}{(b\phi(n))^b - a^b})^a , where a a and b b are coprime positive integers, find a + b a + b .

Note: ϕ ( 4 ) \phi(4) is the golden ratio. Refer to previous problem


The answer is 5.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jan 24, 2019

V s ( 1 ) = 4 3 π R 1 3 V_{s}(1) =\dfrac{4}{3}\pi R_{1}^3 .

x = 2 r 1 sin ⁡ ( π n ) x = 2r_{1}\sin(\dfrac{\pi}{n}) and h = r 1 cos ⁡ ( π n ) ⟹ A △ A B C = n 2 sin ⁡ ( 2 π n ) r 1 2 ⟹ V 1 ( p ) = n 6 sin ⁡ ( 2 π n ) r 1 2 H 1 h = r_{1}\cos(\dfrac{\pi}{n}) \implies A_{\triangle_{ABC}} = \dfrac{n}{2}\sin(\dfrac{2\pi}{n})r_{1}^2 \implies V_{1}(p) = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})r_{1}^2H_{1}

R 1 2 = ( H 1 − R 1 ) 2 + r 1 2 ⟹ r 1 2 = 2 H 1 R 1 − H 1 2 ⟹ V 1 = n 6 sin ⁡ ( 2 π n ) ( 2 H 1 2 R 1 − H 1 3 ) ⟹ R_{1}^2 = (H_{1} - R_{1})^2 + r_{1}^2 \implies r_{1}^2 = 2H_{1}R_{1} - H_{1}^2 \implies V_{1} = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})(2H_{1}^2R_{1} - H_{1}^3) \implies d V 1 ( p ) d H 1 = n 6 sin ⁡ ( 2 π n ) H 1 ( 4 R 1 − 3 H 1 ) = 0 ⟹ H 1 = 4 R 1 3 ⟹ r 1 = 2 2 3 R 1 \dfrac{dV_{1}(p)}{dH_{1}} = \dfrac{n}{6}\sin(\dfrac{2\pi}{n})H_{1}(4R_{1} - 3H_{1}) = 0 \implies H_{1} = \dfrac{4R_{1}}{3} \implies r_{1} = \dfrac{2\sqrt{2}}{3}R_{1}

s = h 2 + H 1 2 = 2 2 3 cos ⁡ 2 ( π n ) + 2 R 1 s = \sqrt{h^2 + H_{1}^2} = \dfrac{2\sqrt{2}}{3}\sqrt{\cos^2(\dfrac{\pi}{n}) + 2}R_{1}

The area of the above triangle is A = h H 1 = ( h + s ) R 2 ⟹ R 2 = h H 1 h + s A = hH_{1} = (h + s)R_{2} \implies R_{2} = \dfrac{hH_{1}}{h + s}

h H 1 = 8 2 9 cos ⁡ ( π n ) R 1 2 hH_{1} = \dfrac{8\sqrt{2}}{9}\cos(\dfrac{\pi}{n})R_{1}^2 and h + s = 2 2 3 ( cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 ) R 1 ⟹ h + s = \dfrac{2\sqrt{2}}{3}(\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2})R_{1} \implies R 2 = 4 cos ⁡ ( π n ) R 1 3 ( cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 ) R_{2} = \dfrac{4\cos(\dfrac{\pi}{n})R_{1}}{3(\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2})}

Let a n = cos ⁡ ( π n ) cos ⁡ ( π n ) + cos ⁡ 2 ( π n ) + 2 = a_{n} = \dfrac{\cos(\dfrac{\pi}{n})}{\cos(\dfrac{\pi}{n}) + \sqrt{\cos^2(\dfrac{\pi}{n}) + 2}} = 1 1 + 1 + 2 sec ⁡ 2 ( π n ) \dfrac{1}{1 + \sqrt{1 + 2\sec^2(\dfrac{\pi}{n})}}

Now let ϕ ( n ) = 1 + 1 + 2 sec ⁡ 2 ( π n ) 2 ⟹ j ( n ) = 4 3 a n = 2 3 ϕ ( n ) ⟹ R 2 = j ( n ) R 1 = 2 3 ϕ ( n ) R 1 \phi(n) = \dfrac{1 + \sqrt{1 + 2\sec^2(\dfrac{\pi}{n})}}{2} \implies j(n) = \dfrac{4}{3}a_{n} = \dfrac{2}{3\phi(n)} \implies R_{2} = j(n)R_{1} = \dfrac{2}{3\phi(n)}R_{1}

and ⟹ r 2 = 2 2 3 R 2 = 2 2 3 ( 2 3 ϕ ( n ) ) R 1 \implies r_{2} = \dfrac{2\sqrt{2}}{3}R_{2} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})R_{1} , H 2 = 4 3 R 2 = 4 3 ( 2 3 ϕ ( n ) ) R 1 , \:\ H_{2} = \dfrac{4}{3}R_{2} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})R_{1}, R 3 = 2 3 ϕ ( n ) R 2 = ( 2 3 ϕ ( n ) ) 2 R 1 , \:\ R_{3} = \dfrac{2}{3\phi(n)}R_{2} = (\dfrac{2}{3\phi(n)})^2R_{1}, r 3 = 2 2 3 R 3 = 2 2 3 ( 2 3 ϕ ( n ) ) 2 R 1 , \:\ r_{3} = \dfrac{2\sqrt{2}}{3}R_{3} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})^2R_{1}, H 3 = 4 3 R 3 = 4 3 ( 2 3 ϕ ( n ) ) 2 R 1 \:\ H_{3} = \dfrac{4}{3}R_{3} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})^2R_{1}

In General:

R m = ( 2 3 ϕ ( n ) ) m − 1 R 1 R_{m} = (\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

r m = 2 2 3 ( 2 3 ϕ ( n ) ) m − 1 R 1 r_{m} = \dfrac{2\sqrt{2}}{3}(\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

h m = 4 3 ( 2 3 ϕ ( n ) ) m − 1 R 1 h_{m} = \dfrac{4}{3}(\dfrac{2}{3\phi(n)})^{m - 1}R_{1}

⟹ V s ( m ) = ( 8 27 ϕ ( n ) ) m − 1 V s ( 1 ) \implies V_{s}(m) = (\dfrac{8}{27\phi(n)})^{m - 1}V_{s}(1) and V p ( m ) = 4 27 π n sin ⁡ ( 2 π n ) ( 8 27 ϕ ( n ) ) m − 1 V s ( 1 ) V_{p}(m) = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{8}{27\phi(n)})^{m - 1}V_{s}(1)

⟹ \implies

V s = V s ( 1 ) ∑ m = 1 ∞ ( 8 27 ϕ ( n ) ) m − 1 = 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 V s ( 1 ) V_{s} = V_{s}(1)\sum_{m = 1}^{\infty} (\dfrac{8}{27\phi(n)})^{m - 1} = \dfrac{27\phi^3(n)}{27\phi^3(n) - 8}V_{s}(1)

and

V p = 4 27 π n sin ⁡ ( 2 π n ) ( 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 ) V s ( 1 ) V_{p} = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{27\phi^3(n)}{27\phi^3(n) - 8})V_{s}(1)

⟹ V s ∗ V p V s ( 1 ) 2 = 4 27 π n sin ⁡ ( 2 π n ) ( 27 ϕ 3 ( n ) 27 ϕ 3 ( n ) − 8 ) 2 = 2 2 3 3 π n sin ⁡ ( 2 π n ) ( ( 3 ϕ ( n ) ) 3 ( 3 ϕ ( n ) ) 3 − 2 3 ) 2 = a a b b π n sin ⁡ ( 2 π n ) ( ( b ϕ ( n ) ) b ( b ϕ ( n ) ) b − a b ) a \implies \dfrac{V_{s} * V_{p}}{V_{s}(1)^2} = \dfrac{4}{27\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{27\phi^3(n)}{27\phi^3(n) - 8})^2 = \dfrac{2^2}{3^3\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{(3\phi(n))^3}{(3\phi(n))^3 - 2^3})^2 = \dfrac{a^a}{b^b\pi}n\sin(\dfrac{2\pi}{n})(\dfrac{(b\phi(n))^b}{(b\phi(n))^b - a^b})^a ⟹ a + b = 5 \implies a + b = \boxed{5}

Note: For nested cones and spheres we have: α = lim ⁡ n → ∞ ϕ ( n ) = 1 + 3 2 \alpha = \lim_{n \rightarrow \infty} \phi(n) = \dfrac{1 + \sqrt{3}}{2} and lim ⁡ n → ∞ n sin ⁡ ( 2 π n ) = 2 π \lim _{n \rightarrow \infty} n\sin(\dfrac{2\pi}{n}) = 2\pi .

Letting P ( n ) = V s ( n ) ∗ V p ( n ) V s ( 1 ) 2 ⟹ lim ⁡ n → ∞ P ( n ) = 8 27 ( 27 α 3 27 α 3 − 8 ) 2 P(n) = \dfrac{V_{s}(n) * V_{p}(n)}{V_{s}(1)^2} \implies \lim_{n \rightarrow \infty} P(n) = \dfrac{8}{27}(\dfrac{27\alpha^3}{27\alpha^3 - 8})^2 .

My problem for Nested square pyramids and spheres

My problem for Nested Tetrahedrons and spheres

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...