Nested Triangles
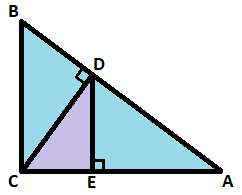
In the diagram, ∠ A C B , ∠ A E D , and ∠ B D C are right angles, C D = 6 0 , and the area of △ A B C is 3 7 5 0 .
Find the perimeter of △ C D E .
The answer is 144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Nice solution!
@David Vreken
This way, we can find out sin(2A) and use it to solve this problem. Pardon me for the slapdash diagram, but you get the idea...
Wow, fantastic diagram and solution! Thanks for sharing.
If the area of the entire triangle is 3 7 5 0 , then we have that 2 C D × B A = 3 7 5 0 = > 2 6 0 × B A = 3 7 5 0 = > B A = 6 0 3 7 5 0 × 2 = 1 2 5 .
We know that A C × B C = C D × B A = 6 0 × 1 2 5 . Rearranging we get 6 0 A C × B C = 1 2 5 . However, we also know by Pythagorean theorem that A C 2 + B C 2 = B A = 1 2 5 . At this point, I graphed the two functions ( 6 0 x × y = 1 2 5 and x 2 + y 2 = 1 2 5 ) and found that the intersect each other at ( 7 5 , 1 0 0 ) . So now we know that B C = 7 5 and A C = 1 0 0 .
Next, we can look at the leftmost triangle. To find B D , we can use Pythagorean theorem. B D = B C 2 − D C 2 = 7 5 2 − 6 0 2 = 4 5 . We can subtract this from B A to find D A : D A = B A − B D = 1 2 5 − 4 5 = 8 0 .
We also know that C A × D E = C D × D A . Rearranging to find D E , we get that D E = C A C D × D A = 1 0 0 6 0 × 8 0 = 4 8 .
Finally, we can use Pythagorean theorem on the purple triangle: C D = C D 2 − D E 2 = 6 0 2 − 4 8 2 = 3 6 .
Therefore, the perimeter of C E D is 6 0 + 4 8 + 3 6 = 1 4 4 .
Nice solution!
From the given informations, we get sin(2A)=0.96. Therefore sin(A)=0.6, cos(A)=0.8 Hence perimeter of the triangle CDE is 60(1+sin(A)+cos(A))=144
How do you know sin(2A) = 0.96?
Log in to reply
BC=60secA, CE=60sinA, DE=60cosA, EA=60cosAcotA. Therefore CA=CE+EA=60cosecA. Area of the triangle ABC is (1/2)(BC) (CA). This gives (60secA) (60cosecA)=(2)(3750)=7500, or sinAcosA=12/25 or sin(2A)=24/25=0.96
I'll start with the observation that A B = 1 2 5 , given the values of C D = 6 0 and the area of triangle △ A B C = 3 7 5 0 .
Let x = B D . Then A D = 1 2 5 − x , and given the similarity of triangles △ B D C and △ C D A , we see that x 6 0 = 6 0 1 2 5 − x .
Cross-multiplying leads to 3 6 0 0 = x ( 1 2 5 − x ) , a quadratic equation with solutions x = 4 5 and x = 8 0 . (Aside: the picture suggests that our value of x is the lesser of these two values, but we cannot infer that choice from the information provided. Pictures cannot be used to infer information not explicitly provided. )
If we let x = 4 5 , then we see that all the triangles are similar, with leg proportions in a 3 : 4 : 5 ratio. This leads to (calculations omitted) B C = 7 5 , A E = 6 4 , C E = 3 6 , and D E = 4 8 , with the perimeter of △ C D E = 3 6 + 4 8 + 6 0 = 1 4 4 .
If, however, x = 8 0 , then the proportions on all the triangles are swapped, with the previously shorter legs now the longer legs. This leads to B C = 1 0 0 , A E = 2 7 , C E = 4 8 , and D E = 3 6 . In this case we also get that the perimeter of △ C D E = 3 6 + 4 8 + 6 0 = 1 4 4 .
Nice solution! This is pretty much the same way that I solved it.
Thanks, David!
Area of triangle ABC = 3750 = (1/2) 60 (BA), so BA = 125. Define BD = x and <DCB = <CDE = <BAC = t. BC = sqrt(3600 + x^2). sin(t) = x/sqrt(3600 + x^2) = sqrt(3600 + x^2)/125. Cross-multiplying, x^2 -125x + 3600 = 0, or (x - 45)(x - 80) = 0, so x = 45 or x = 80. If x = 80, DC = 60, BC = 100, sin(t) = (CE)/60 = 80/100 = .8, and CE = 48,DE = 36, and DE + CE + DC = 144. If x = 45, DC = 60, BC = 75. Sin(t) = 75/125 = .6, = CE /60, and CE = 36. Then DE = 48, and DE + CE + DC = 144.
Nice solution!
David, thank you
Let ∠ A = t and let A B = h , then C D = 6 0 = h cos t sin t , and [ A B C ] = 3 7 5 0 = 2 1 h 2 cos t sin t . Dividing the second equation by the first equation, yields, h = 125, from which cos t sin t = 2 1 sin ( 2 t ) = 6 0 / 1 2 5 , or sin ( 2 t ) = 2 4 / 2 5 , and this means that cos ( 2 t ) = 2 5 2 − 2 4 2 / 2 5 = 2 5 7 . This in turn implies that cos t = ( 1 + cos 2 t ) / 2 = 2 1 ( 1 + 2 5 7 ) = 5 4 , and therefore, sin t = 5 3 . Now D E = C D cos t = 6 0 ( 4 / 5 ) = 4 8 , and C E = C D sin t = 6 0 ( 3 / 5 ) = 3 6 , so perimeter = 6 0 + 4 8 + 3 6 = 1 4 4 .
Great solution!
We note that △ A B C , △ B C D , and △ C D E are similar. Let B C = a , C A = b , and A B = c . From similar triangles,
C A A B b c ⟹ c = 6 0 B C = 6 0 a = 6 0 a b = 6 0 7 5 0 0 = 1 2 5 Note that [ A B C ] = 2 a b = 3 7 5 0
Then we have [ A B C ] [ C D E ] = 1 2 5 2 6 0 2 , ⟹ [ C D E ] = 1 2 5 2 6 0 2 × 3 7 5 0 = 8 6 4 . Let E C = x and D E = y . Then
⎩ ⎨ ⎧ 2 x y = 8 6 4 ⟹ y = x 1 7 2 8 x 2 + y 2 = 6 0 2 = 3 6 0 0 . . . ( 1 ) . . . ( 2 )
From ( 2 ) :
x 2 + x 2 1 7 2 8 2 x 4 − 3 6 0 0 x 4 + 2 9 8 5 9 8 4 ( x 2 − 1 2 9 6 ) ( x 2 − 2 3 0 4 ) = 3 6 0 0 = 0 = 0 Substituting y = x 1 7 2 8 Rearranging and solving the quadratic for x 2
⟹ x = { 3 6 = E C 4 8 = D E . Therefore the perimeter of △ C D E is C D + D E + E C = 6 0 + 4 8 + 3 6 = 1 4 4 .