Nesting Shapes
I begin with a circle of radius 1 cm , which becomes the inscribed circle of an equilateral triangle, which I enclose with its circumcircle (the circle that touches all of its vertices). I enclose this circle with a square (so that each edge touches the circle once), and surround this with the square's circumcircle. I repeat this procedure with a pentagon, a hexagon, and so on forever (increasing the side number by one, until we reach an infinity-sided polygon).
What is the limiting area (in cm 2 ) of the "final" circle, rounded to a whole number?
The answer is 238.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How did you solve the series ?
Log in to reply
I don't have a problem with this solution's use of brute force. (In case anyone is wondering, you need to go a bit past 8,000 sides in order to get the correct answer.) However, in order for the solution to be complete I think you need to justify it -- e.g. how do you know that going to 80,000 sides, or 8*10^30 sides, won't yield an area of 239?
Unfortunately you have to brute force it :( I used Wolfram Alpha.
Log in to reply
I used wolfram alpha too, is there no otherway around the bruteforce?
Frankly, the lack of elegance in problems like this detracts from my personal experience on Brilliant. I just don't find it rewarding to multiply sec(π/n) for arbitrarily large n. It doesn't make me feel clever by finding neat patterns or noticing that the answer is hidden right in front of me, like in most other problems on the site. This kinda just feels like a drab homework problem you'd be assigned in a high school pre-calculus class. Not a high quality problem in my opinion.
So no way to solve using pen and paper?
If you know about Kepler–Bouwkamp constant , which is approximately equal to 8 7 1 0 , you can follow a similar logic to derive the infinite product, as in Fin Moorhouse's solution, to get the Polygon Circumscribing Constant , which happens to be the reciprocal of Polygon Inscribing Constant . Using the constant, you can find the area.
Thanks for posting- I had never heard of that!
Not knowing difficult formulae as a layman, it is better to work out how the radius grows first. Making use of trigonometry, one should find the radius of the 'final' circle = 1/(sin30° * sin45° * sin54°) ... = 1/Π(sin((n-2) 180°/(2n))), from n=3 to ∞ Converting degrees to radians by multiplying π/180° with the term inside the sine function, we have the infinite product formula for the radius to be solved by Wolfram Alpha: Product[1/sin(0.5 (n-2)*pi/n), {n, 3, Infinity}], which gives us the limiting radius ≈ 8.70004cm ∴ Area of circle = 237.78933450372489696107511686176... ≈ 238 c m 2
So there is no manually computable solution to this problem?
I did get the equation to the solution: A = ( n → ∞ lim i = 4 ∏ n cos i π ) 2 4 π
But then I solved it in Excel as I couldn't figure out how to calculate the limit, hoping I'd learn the real solution here. So are we really saying that there are convergent series to which we can't calculate the limit? (And if that's the case, then this question should obviously be removed from the challenge.)
In order to find the answer, we must find a general equation for the ratio between the area of the inscribed circle of an n-sided polygon, and its circumcircle. Since the area of a circle is π r 2 , we should find the radii of the two circles. Consider the diagram: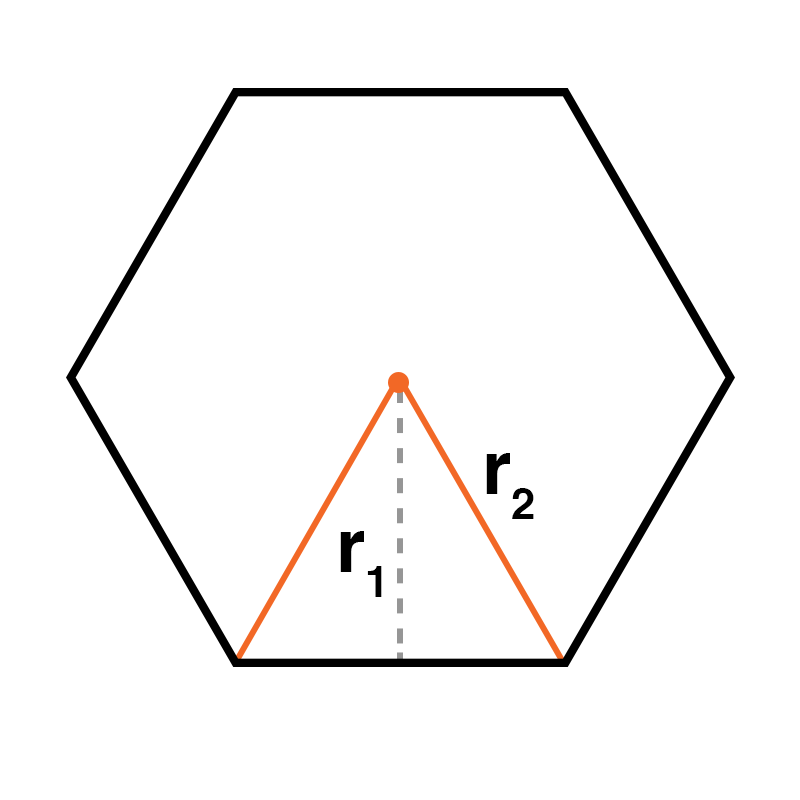
A hexagon is used as an example, but this applies to all regular n-sided polygons. The radius of the inner circle will be R 1 , and that of the outer circle will be R 2 . If we take R 1 to be 1, then R 2 will be equal to c o s ( 2 n 3 6 0 ) 1 , since c o s ( θ ) = h y p o t e n u s e a d j a c e n t and the angle in question will be equal to 2 n 3 6 0 . Thus, the ratio of the area of the outer circle to the area of the inner circle of any n-sided regular polygon will be c o s ( 2 n 3 6 0 ) 1 2 : 1 (the π s in π r 2 cancel. This cancels to s e c 2 ( n 1 8 0 ) , which looks a bit nicer. The first regular polygon that we need to deal with has three sides, so the area of the triangle's outer circle is sec 2 ( 3 1 8 0 ) = 4 times bigger than the inner circle. We can multiply the ratios of the infinite remaining circles together in a similar way, increasing n by one every time, in order to give the ratio of the area of the very first triangle to the very 'last'. This gives the infinite, convergent product ∏ n = 3 ∞ s e c 2 ( n 1 8 0 ) , which is roughly equal to 7 5 . 7 . To reach the final answer, we simply multiply the area of the first circle ( π c m 2 ) by this result, giving us ( ∏ n = 3 ∞ s e c 2 ( n 1 8 0 ) ) ∗ π ≈ 2 3 8 c m 2 .