Net Perimeter
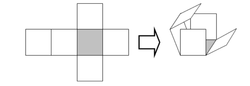The net above can be folded-up to produce a cube and it can be verified that the
perimeter of this particular net is 14 units.
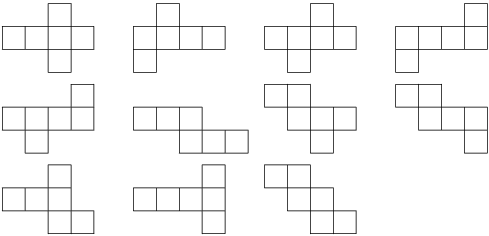
Altogether there are eleven distinct nets that can fold to produce a cube. What is the maximum perimeter possible for any of these eleven nets?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can do this in reverse, and start with a square face, and attach more squares to the net. We have to add 5 more squares. Hence, there has to be a minimum of 5 creases. The total number of edges is 6 x 4 = 24, but each crease removes 2 from the perimeter. Hence, 24 - 2(5) = 14, answer.