Network Theory, Squaring the Square, and the Four Color Theorem: the Diverse Neighborhood
Warning, Apology, and Enticement: I DON'T YET HAVE THE ANSWER TO THIS PROBLEM!
In creating a stained glass panel, I decided to use as the design the lowest order perfect squared square, (see Wikipedia article "Squaring the Square"). That drawing, shown below, is a square subdivided into 21 smaller squares discovered in 1978 by A. J. W. Duijvestijn. The graphic provided here approximates that square. The number in or near each small square identifies it and is the length of one side of that square. (Minor discrepancies are my failings.)
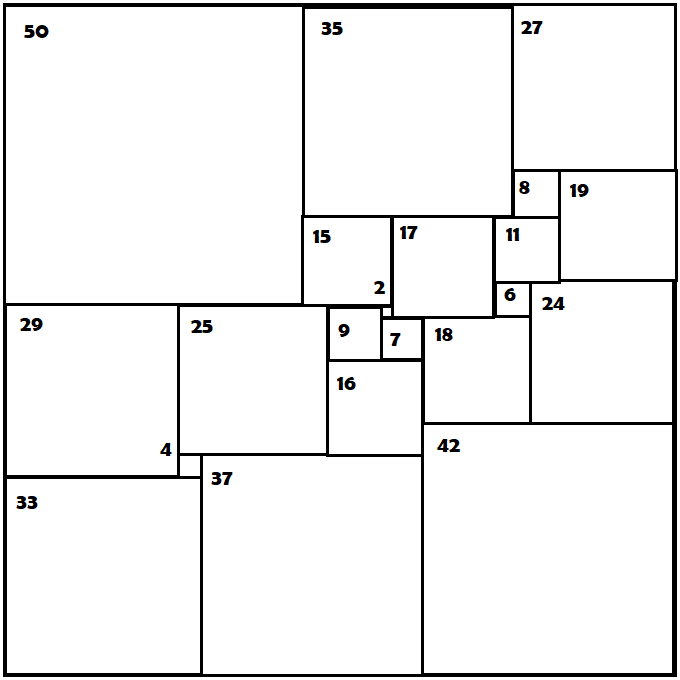
In choosing the glass colors, I decided to demonstrate the four color theorem (see Wikipedia article "Four Color Theorem") by using only four colors of glass, but placing them so that no two neighbors have the same color. I easily found multiple solutions to avoid boundary violations.
Question 1: Is the number of 4 color solutions knowable by any elegant method?
It then occurred to me to add a level of difficulty. Question 2: Could a four color solution be found that had diverse neighbors? Diverse neighbors means the following: could every square in the design have at least one neighbor of each of the other three colors? I observe that every square in this design has at least three neighbors, so a solution could not be ruled out as might happen on a geographical map where some territory has two or fewer borders. Through trial and error, I found three solutions that have only one square which is "not diversified," that is to say, having only two colors as neighbors. Those three maps left squares 2, 27, or 29 not diversified.
Question 3: Is there a way to leave any given square unsatisfied?
A productive technique to experiment is to import the graphic to a paint program and fill squares with colors. Assigning a number to each square in the graphic is helpful in referencing them with a collaborator.
It is also may be helpful to recognize that two squares (33 and 27) have only three neighbors. They have fewer degrees of freedom in achieving diversity. Other squares have more neighbors (square 17 has seven neighbors), which makes them more challenging to avoid a boundary clash by matching the color of a neighbor. Thus, the two goals (4 color and diverse neighbors) creates competing pressure in color assignment.
My instinct is there is no solution better than a single unsatisfied square. Failing to learn of a perfect solution, I will use my favorite with square 2 not diversified, as it is the tiniest square and close to the center. Question 4: Is it provable that there is no complete solution?
If that isn't hard enough, should you find a solution, you deserve extra credit if you can keep the colors balanced: that means each color is used 5 or 6 times. I suppose a tie breaker would lean toward a solution that was best balanced in total area given to each color!
This is a fertile problem for developing more questions, but for me at least, only tantalizing in producing answers. It could be addressed through brute force by computing every combination and grading its boundaries. Inelegant, but know that Duijvestijn used a computer in finding his square, and the Four Color Theorem was the first mathematical proof done with a computer!
Tangential thought: Rather than worry about boundaries matching, I tried to balance the total area each color was used. That involved squaring the number in the graphic on a spreadsheet, then assigning a color to each square and totaling each colors assigned area, to get evenness. With a four color scheme, I had a variance of 24 units of area out of 12544. Using a five color scheme, I had a variance of 22.8 units of area out of 12544. Question 5: What is the minimum variance? Variance, as I perceive it, is a sum of the absolute values of the area used by each color less the area of the total square divided by the number of colors uses. (Visually, these solutions are less satisfying to me, so I did not pursue them further.)
Should you go down this rabbit hole, you will want to see the YouTube article on the Numberphile channel: "Squared Squares - Numberphile" featuring Dr. James Grime as well as his article "The Four Color Map Theorem - Numberphile." It was only after seeing these a few minutes ago, that I realized the rigorous solution is likely found in network theory. As soon as I can, I will post my approach to solving this problem in the discussion.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
My approach to finding a solution is to focus on the two squares with the fewest degrees of freedom: 33 and 27 having only three neighbors each. For those squares in turn, I arbitrarily assigned a color and then assigned colors to their neighbors to see what decisions were forced. I include a graphic in this process: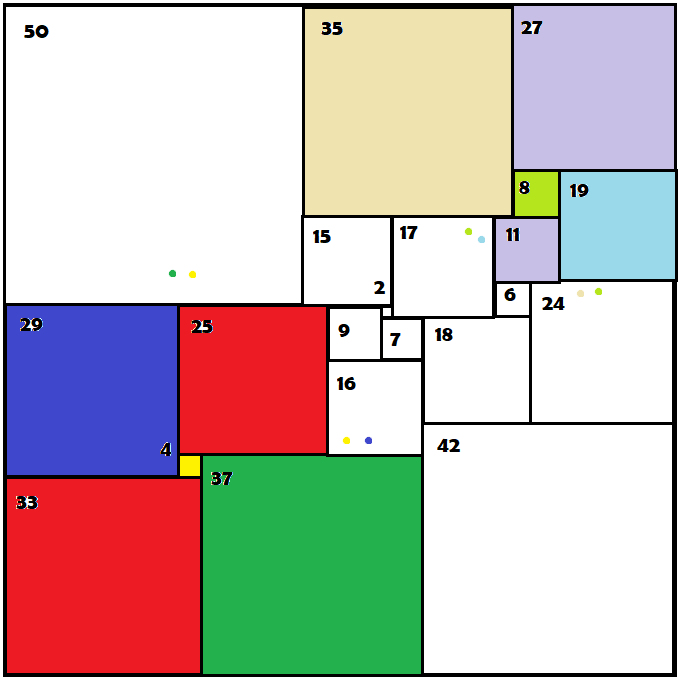
You will note that there are more than 4 colors! Not to worry, it's only temporary. I am simultaneously pursuing two paths of thought. The first, which began with square 33 shows a "primary" color palette of four colors. The second path, which began with square 27 shows a "pastel" color palette. Doing this prevents confusing the two. But when they meet, the two palettes could merge into one palette of four colors more easily. So 27 (lilac) could eventually become red, blue, yellow, or green depending on what I learn when the two palettes meet.
You will also note small dabs of colors in some white squares. Those reveal the only possible results based on currently assigned neighbor colors. (If you play SUDOKU, you may use a similar approach to annotating that puzzle.)
The next step is to try one of the two dabs in a square and see where it leads me. By example, 17 must be chartreuse or robin's egg. Picking robin's egg (arbitrarily) I am left with 6 getting a dab of chartreuse and tan. (So I don't forget, I left the chartreuse dab in 17, as that is still possible.) Aha! If 6 AND 24 have the same two dabs, then 18 must be lilac whenever 17 is robin's egg....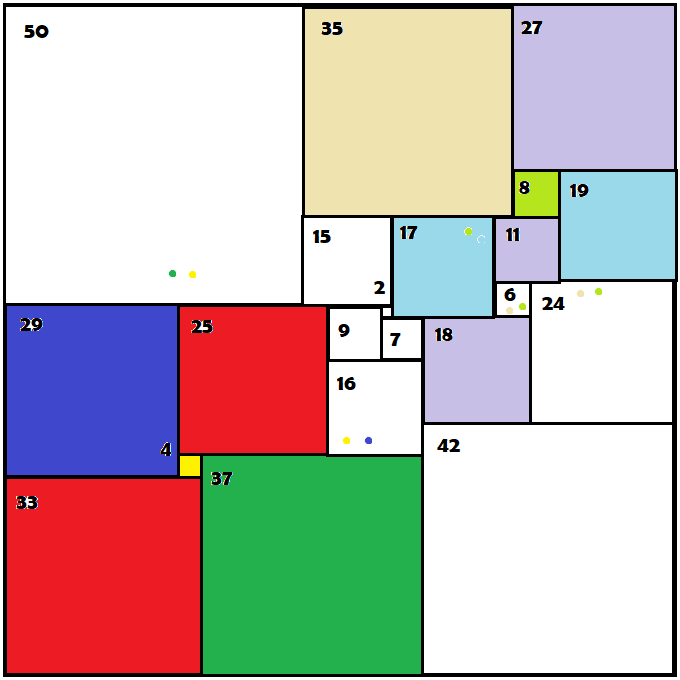
This is not yet a solution of course, but it shows one approach to a solution that organizes the progress. I hope a brighter mind will see farther.