Neutrinos through the earth
Neutrinos are interesting little fundamental particles. These particles interact very weakly with everything else, so they essentially pass right through everyday stuff. In fact there are tremendous numbers of neutrinos passing through your body at this very second! In 2011, two experiments in Italy measured the time it took for neutrinos generated at a particle accelerator at CERN in Geneva, Switzerland to get to a pair of detectors built into the Gran Sasso mountain in central Italy. One of them mistakenly measured the speed as faster than the speed of light, which caused a furor .
The straight line distance through the earth from x 0 , the point of production of the neutrinos at CERN, to x 1 , the point of measurement at Gran Sasso was roughly 7 3 2 km . Now let D be the shortest distance between x 0 and x 1 over the surface of the earth, which is the path we'd have to take if we wanted to get from CERN to Gran Sasso without heavy machinery.
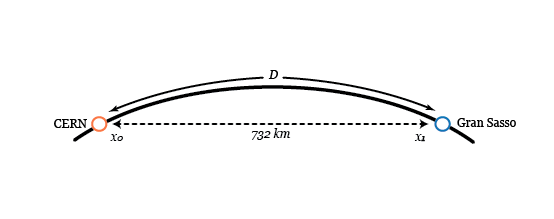
How much longer is D than the neutrino path, i.e. what is D − 7 3 2 km in meters ?
Details and assumptions
You may assume that x 0 and x 1 are on the surface of the earth and that the earth is a perfect sphere of radius 6 , 3 7 0 km .
The answer is 403.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Just a note that the angles are in radians.
Let E represent the center of the Earth, C represent the location of CERN, and G represent Gran Sasso mountain. Note that ∆ ECG is an isosceles triangle such that c and g , segments opposite of points C and G , respectively, are legs formed by radii extending from the center of the Earth. Therefore, c = g = 6370 km and e = 732 km, the straight-line distance between points C and G . Define θ = m ∠ E so that by the law of cosines,
e 2 = c 2 + g 2 − 2 c g cos θ
7 3 2 2 = 6 3 7 0 2 + 6 3 7 0 2 − 2 ( 6 3 7 0 ) ( 6 3 7 0 ) cos θ
5 3 5 8 2 4 = 8 1 1 5 3 8 0 0 − 8 1 1 5 3 8 0 0 cos θ
8 1 1 5 3 8 0 0 cos θ = 8 0 6 1 7 9 7 6
θ = arccos 8 1 1 5 3 8 0 0 8 0 6 1 7 9 7 6
θ ≈ 0 . 1 1 4 9 7 7
The arc length from C to G is given by D = 6370 θ ≈ 732.403 km. Therefore, D – 732 ≈ 0.403 km = 403 m.
Firstly,draw out of a full sphere and draw 2 lines from cern and gran sasso to the centre of the circle.Observe now that the area enclosed by the 2 lines now form a sector on the circle. As we known the formula for the arc lenth of a sector is r x thetha where thetha is the angle of the sector. To find the angle all we have to do is some simple trigonometry 0= 2 sin^-1((732x 0.5)/3760) We know this as the triangle can be split into 2 congurent right triangles by circle properties. Lastly,we apply the formula,hence:
D=732.4034km D-732=0.4034km=403.4m
This problem is based off the faster than light neutrino debacle. Anyone know why, experimentally, neutrinos can't go faster than light?
Log in to reply
Because they have mass while light doesn't?
We can model this as a sector of a circle. Consider a circle, centre O , such that it has a radius of 6 , 3 7 0 k m and points x 0 and x 1 on the circumference. Then, by using the cosine rule, we can see that, cos ( ∠ x 0 O x 1 ) = 2 ⋅ 6 3 7 0 0 0 0 2 2 ⋅ 6 3 7 0 0 0 0 2 − 7 3 2 0 0 0 2 cos ( ∠ x 0 O x 1 ) = 0 . 9 9 3 . . . ∠ x 0 O x 1 = 0 . 1 1 4 . . . Hence, the length of the arc D is given by, D = 6 3 7 0 0 0 0 ⋅ 0 . 1 1 4 . . . = 7 3 2 4 0 3 . 3 5 6 5 So the difference between the length of D and the neutrino path to 3 significant figures is, 7 3 2 4 0 3 . 3 5 6 5 − 7 3 2 0 0 0 = 4 0 3