Never tied?

For each game, consider the running lead that Brazil holds over Germany. Every time Brazil scores a goal, the running lead goes up by $1$ . Every time Germany scores a goal, it goes down by $1$ . Any game can be seen as a sequence of coordinates $(1,a_1),(a,a_2),\ldots,(14,a_{14}=2)$ , where $a_n$ is Brazil's lead after the $n$ th goal, and so each $a_{j+1}$ differs from the preceding $a_j$ by $\pm1$ . Call such a sequence a "path".

A game for which the final score is $8\,:\,6$ is a path from $(0,0)$ to $(14,2)$ , which is the number of ways in which $8$ $1$ s and $6$ $-1$ s can be ordered, namely ${14 \choose 8}$ .

A game in which Brazil scores first is a path from $(1,1)$ to $(14,2)$ , which is the the number of ways in which $7$ $1$ s and $6$ $-1$ s can be ordered, namely ${13 \choose 7}$ .

A game in which Brazil scores first, but during which the game is not always in Brazil's favour, is a path where $a_1=1$ and where $a_n=0$ for some $n$ . For any such path, let $m$ be the smallest integer for which $a_m=0$ . Consider the path $(1,b_1),(2,b_2),\ldots,(14,b_{14})$ where $b_j = -a_j$ for $j < m$ and $b_j = a_j$ for $j \ge m$ . This is a path from $(1,-1)$ to $(14,2)$ , and $m$ is the smallest integer for which $b_m=0$ .

Conversely, if we have a path from $(1,-1)$ to $(14,2)$ , there must be at least one time when the current lead is $0$ . Let $m$ be the smallest integer for which $a_m=0$ . By changing the signs of the value of $a_j$ for $j < m$ , we obtain a path from $(1,1)$ to $(14,2)$ which reaches $0$ for the first time at the $m$ th game.

This process of reflection yields a 1-1 correspondence between the paths from $(1,1)$ to $(14,2)$ which reach $0$ and the paths from $(1,-1)$ to $(14,2)$ . The number of paths from $(1,-1)$ to $(14,2)$ is the number of ways in which $8$ $1$ s and $5$ $-1$ s can be ordered, namely ${13 \choose 8}$ .

Thus there are ${13 \choose 7} - {13 \choose 8} = 429$ scoring orders for which Brazil never loses the lead. Dividing this number by ${14 \choose 8}$ gives the answer of $1/7$ .

If the final score was $p\,:\,q$ with $p>q$ , the same argument would give the probability as $\frac{{p+q-1 \choose p-1} - {p+q-1 \choose p}}{{p+q \choose p}} \; = \; \frac{p-q}{p+q} \;.$

In a game where Brazil wins and the game is never tied, Brazil must score the first two goals. From a score of 2-0, the game must end with a score of 8-6. This is equivalent to the number of lattice paths from (2, 0) to (8, 6) that do not such the main diagonal $(n, n)$ , which is equivalent to the number of lattice paths from (0, 0) to (6, 6) that do not touch the diagonal $(n - 2, n)$

Here is me being lazy:

Basically each cell is calculated as (cell to the left) + (cell above). In the top half, I forced everything on or below the diagonal to be zero. The answer is the ratio between the highlighted numbers, $\frac{429}{3003} = \tfrac17 = \boxed{0.142857}.$

For a more elegant solution, use Catalan numbers. In this case, the answer is $\frac{C_7}{\text{total paths}} = \frac{\frac{1}{7+1}\left(\begin{array}{c} 2\cdot 7 \\ 7\end{array}\right)}{\left(\begin{array}{c} 6+8 \\ 6\end{array}\right)} = \frac{\left(\frac{14\cdot13\cdot12\cdot11\cdot10\cdot9}{7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}\right)}{\left(\frac{14\cdot13\cdot12\cdot11\cdot10\cdot9}{6\cdot5\cdot4\cdot3\cdot2\cdot1}\right)} = \frac{1}{7}.$

Indeed we can apply Bertrand's ballot theorem here.

In general, if Brazilians scores p goals, Germans score q goals, and p>q , then the probability that the game was never tied is $\frac {p-q}{p+q}$ .

In our case this is $\frac{8-6}{8+6} = \boxed{\frac17}$ .

Part 1: number of correct sequences

Brazil scores first. If we don't count this first goal, the number of ways is the same as having 7 goals for Brazil and 6 for Germany, providing that Germany never scores more than Brazil at any point (same rule as original question, but now with equality allowed). But that is the same as the number of ways to have 7 goals of each country, with the same new rule, because in this new case 7–7, Germany would have to score the last goal.

Now, what is the number of ways to put 7 goals of each of the two teams in a row, without Germany to ever lead? This is given by the 7th Catalan number , which is $C_n=\frac{1}{n+1}{2n \choose n}$ with $n=7$ , which gives $C_7=\frac{1}{8}\cdot\frac{14!}{7!\cdot 7!}=\boxed{\frac{14!}{8!\cdot 7!}}$ .

Part 2: number of sequences

It's the number of ways to put 8 B and 6 G in a row, which is ${14 \choose 8}=\boxed{\frac{14!}{8!\cdot 6!}}$

Answer

Probability is the ratio $\displaystyle{\frac{\ \ \ \frac{14!}{8!\cdot 7!}\ \ \ }{\ \ \ \frac{14!}{8!\cdot 6!}\ \ \ }=\frac{6!}{7!}=}\ \boxed{\displaystyle{\frac{1}{7}}^{\ }_{\ }\!}$ .

---

Generalization

By the same proof, it's easy to show that with $n+1$ goals for Brazil and $n-1$ goals for Germany, the probability is $\frac{1}{n}$ .

This problem can be treated as a random walk. Consider $S=\{s=(b,g) | 0 \leq b \leq 8, 0\leq g \leq 6\}$ to be the set of all the possible states. The set of states in which the game is tied is $T \subset S$ such that $T=\{t=(b,g) | b=g\}$ . We have to find the probability $P$ that the game is never tied, that is

$\displaystyle P=\frac{|\text{path}(S\setminus T)|}{|\text{path}(S)|}$

where $|\text{path}(S)|$ are the paths from $(0,0)$ to $(8,6)$ through the points in $S$ .

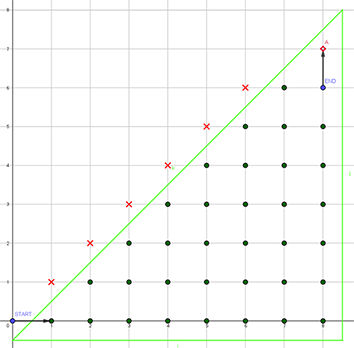
The situation can be represented on the cartesian plane where the green points are the non-tied states of the game, the red crosses the states in which the game is tied. Notice that the points of the kind $(b,g)$ such that $0 \leq g \leq 8$ , $b < g$ are not indicated since if the game happens to end in such states, there is no way to reach $(8,6)$ without crossing one of the red points.

Now, we have that

$\displaystyle |\text{path}(S)|=\binom{14}{8}=\binom{14}{6}$

We do a consideration about $\text{path}(S\setminus T)$ : the number of paths from $(0,0)$ to $(8,6)$ avoiding the red points is equal to the number of pa()ths from $(1,0)$ to $(8,7)$ since the first transition $(0,0) \to (1,0)$ and the last $(8,6) \to (8,7)$ are obliged. The number of such paths is given by the Catalan numbers for $n=7$ . That is,

$\displaystyle |\text{path}(S\setminus T)|=C_n=\frac{1}{n+1}\binom{2n}{n}=\frac{1}{8}\binom{14}{7}$

Eventually

$\displaystyle P=\frac{|\text{path}(S\setminus T)|}{|\text{path}(S)|}=\frac{1}{8}\binom{14}{7} \binom{14}{8}^{-1}=\frac{1}{7}\approx \boxed{0.14285}$

Consult Bertrand's Ballot problem.U will get $\frac{8-6}{8+6}$ = $\frac{1}{7}$ .