New Five Incircles Revolution!
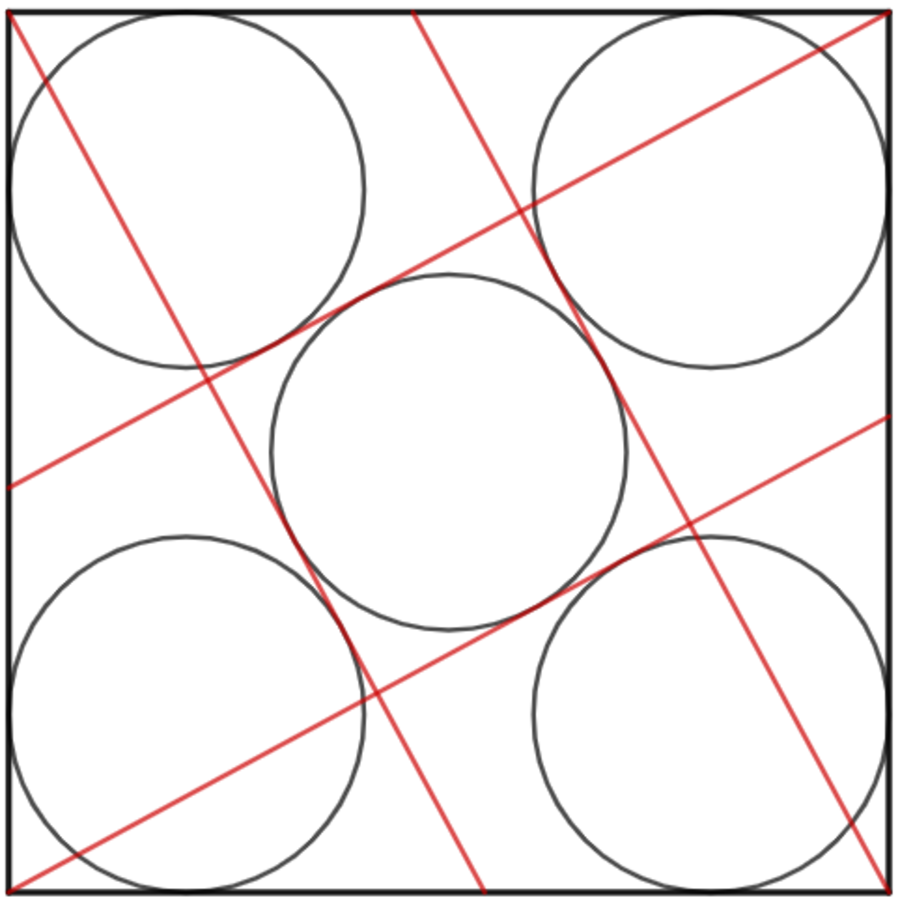
Five identical circles are positioned inside the unit square. Each of the four incircles is tangent to one of the four red lines, whereas one circle is positioned inside the square.
If the radius of the circle is r , input ⌊ 1 0 5 r ⌋ as your answer.
The answer is 20196.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Label the diagram as follows, and let A F = E D = k :
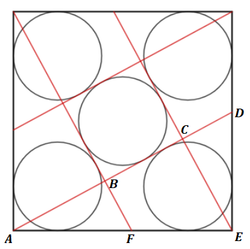
By the Pythagorean Theorem on △ A D E , A D = D E 2 + A E 2 = k 2 + 1 .
Since △ A B F ∼ △ A E D by AA similarity, A B = A F ⋅ A D A E = k ⋅ k 2 + 1 1 = k 2 + 1 k and B F = A F ⋅ A D D E = k ⋅ k 2 + 1 k = k 2 + 1 k 2 = C D .
Then B C = A D − A B − C D = k 2 + 1 − k 2 + 1 k − k 2 + 1 k 2 = k 2 + 1 1 − k .
As an incircle of the red square, r = 2 1 B C = 2 1 ⋅ k 2 + 1 1 − k = 2 k 2 + 1 1 − k .
As an incircle of right △ A D E , r = 2 1 ( D E + A E − A D ) = 2 1 ( k + 1 − k 2 + 1 ) .
So r = 2 k 2 + 1 1 − k = 2 1 ( k + 1 − k 2 + 1 ) , which solves numerically to r ≈ 0 . 2 0 1 9 6 4 and k ≈ 0 . 5 4 0 7 9 0 .
Therefore, ⌊ 1 0 5 r ⌋ = 2 0 1 9 6 .
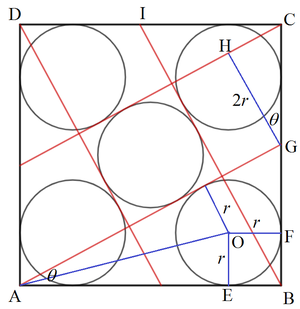
Label the unit square A B C D , red lines A G and B I , the center of the bottom-right circle O . Let O E and O F be perpendicular to A B and B C respectively, and ∠ G A B = θ . We note that
A E + E B O E ⋅ cot 2 ∠ G A B + O F r cot θ 2 + r t r + r ⟹ r = A B = A B = 1 = 1 = t 1 + 1 1 = 1 + t t Let t = tan 2 θ
Due to symmetry, the two pairs of parallel red lines are perpendicular to each other. That is A G ∣ ∣ B I . Let G H ∣ ∣ B I . Then ∠ H G C = θ and:
G H C G ⋅ cos θ ( B C − B G ) cos θ ( 1 − tan θ ) cos θ cos θ − sin θ 1 + t 2 1 − 2 t − t 2 3 t 3 + 3 t 2 + 3 t − 1 ⟹ t r ⟹ ⌊ 1 0 5 r ⌋ = 2 r = 2 r = 2 r = 2 r = 2 r = 1 + t 2 t = 0 ≈ 0 . 2 5 3 0 7 6 5 8 7 = 1 + t t ≈ 0 . 2 0 1 9 6 4 1 8 1 = 2 0 1 9 6 Solving for t by numerical method
Just for drill, I wanted to see if sympy could solve this.