New insight to problem 3, IMO 1973

$P(x)=x^4+ax^3+bx^2+ax+1=0$ Let $(a_0, b_0)$ be a point on the boundary $f$ of set $A$ . We claim that for each point on $f$ like $(a_0, b_0)$ the equation $P(x)=0$ has a multiple root. Because if all the roots of $P(x)=0$ at point $(a_0, b_0)$ be simple, there is a neighborhood of this point where all of roots of $P(x)=0$ are also simple (Because if changes in coefficients are small enough, changes in roots will be very small as well and they remain simple). Therefore, $(a_0, b_0)$ would be a interior point of $A$ and not a boundary point of it. So for each point of $f$ , the equation $P(x)=0$ has at least one multiple root.

Let $|r| \neq 1$ be the multiple root of the polynomial, then $P \left(\frac{1}{r} \right)=\frac{1}{r^4} P(r)=0$ so $\frac{1}{r}$ is a multiple root too. Since product of roots are $1$ they must be $r, r, \frac{1}{r}, \frac{1}{r}$ Hence $\displaystyle \begin{array}{c}\\ P(x) &&= (x-r)^2 \left( x-\frac{1}{r} \right)^2 \\ &&= x^4-2 \left(r+\frac{1}{r} \right) x^3+ \left(r^2+\frac{1}{r^2}+4 \right) x^2 -2 \left(r+\frac{1}{r} \right) x+1 \end{array}$ With substituting $y=r+\frac{1}{r}; |y|>2$ we get $a=-2y, \ \ b=y^2+2$ Eliminating $y$ from these equations gives us $b=\frac{a^2}{4}+2; \ \ |a|>4$ as a part of $f$ .

Now for $|r|=1$ multiple root of $P(x)=0$ is $1$ or $-1$ . In this case $P(1)=2a+b+2=0$ and $P(-1)=-2a+b+2=0$ gives one pair of symmetric lines. Combining these lines for $|a| \le 4$ we get remaining part of $f$ as $b=2|a|-2; \ \ |a| \le 4$ Note that for $|a|>4$ points on the lines $b=2|a|-2$ are interior to set $A$ . So $b 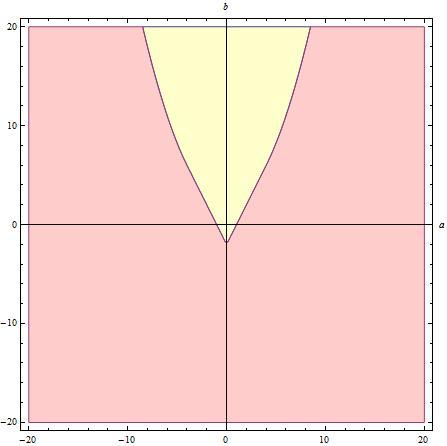=\left\{\begin{array}{lr} \frac{a^2}{4}+2 & \mbox{if } |a|>4 \\ 2 |a|-2 & \mbox{if } |a| \le 4 \end{array} \right.$

Red part of the graph and the boundary (black) form set $A$ and yellow part is $A'$ where all of the roots of $P(x)=0$ are complex. You may think about following conclusions:

1) There is no simple root on the boundary.

2) Set $A'$ has no boundary.

The equation $x^4+ax^3+bx^2+ax+1=0$ has a real solution if and only if the equation $x^2+ax+b+\frac{a}{x}+\frac{1}{x^2}=0$ has a real solution. The latter equation can be written in the form $(x+1/x)^2+a(x+1/x)+b-2=0\:\:\:\:\:\:\:\:(1)$ By making the substitution $u=x+1/x$ we get the equation $u^2+au+b-2=0\:\:\:\:\:\:\:\:(2)$

It is easy to see that $x$ is real if and only if $u$ is real and $|u|\geq2.$ So the problem of finding the region of all pairs $(a, b)$ such that the given equation has at least one real solution reduces to the problem of finding the region of all pairs $(a, b)$ such that the equation (2) has at least one real solution (by the way, in this case both solutions, if they were different, will be real) and at least one solution has absolute value greater than or equal to 2. The latter condition is equivalent to $a^2-4(b-2)\geq 0$ and either $\frac{-a- \sqrt{a^2-4(b-2)}}{2}\leq -2 \text{ or}\: \frac{-a+ \sqrt{a^2-4(b-2)}}{2}\geq 2.$ When $|a|\geq 4$ this implies that one of the two conditions $\frac{-a- \sqrt{a^2-4(b-2)}}{2}\leq -2\: \text {or} \: \frac{-a+ \sqrt{a^2-4(b-2)}}{2}\geq 2$ is going to be true for all values of $b$ such that $a^2-4(b-2)\geq 0$ . Then the upper boundary of the region for any value of $a$ such that $|a|\geq 4$ will be $a^2-4(b-2)= 0,$ or equivalently $b=\frac{a^{2}}{4}+2.$

When $|a|<4,$ the condition $\frac{-a- \sqrt{a^2-4(b-2)}}{2}\leq -2 \:\text{or}\: \frac{-a+ \sqrt{a^2-4(b-2)}}{2}\geq 2$ becomes $b\leq 2a-2$ or $b\leq -2a -2$ , and it is not difficult to see that for those values of $a$ the inequalities $2a-2\leq \frac{a^{2}}{4}+2$ and $-2a-2\leq \frac{a^{2}}{4}+2$ take place.

Therefore, the upper boundary of the region will be $b\leq -2a -2$ for $-4<a\leq 0$ and $b\leq 2a-2$ for $0\leq a<4$ .

That is why the function $f$ is defined by $b=f(a)=\frac{a^{2}}{4}+2$ when $|a|\geq 4$ , $b=f(a)=-2a-2$ if $-4<a\leq 0$ or $b=f(a)=2a-2$ if $0\leq a<4.$ Therefore, $f(7)+f(19/8)=\frac{7^2}{4}+2+2\frac{19}{8}-2=17.$