New Paper Size R4

Algebra Level 4

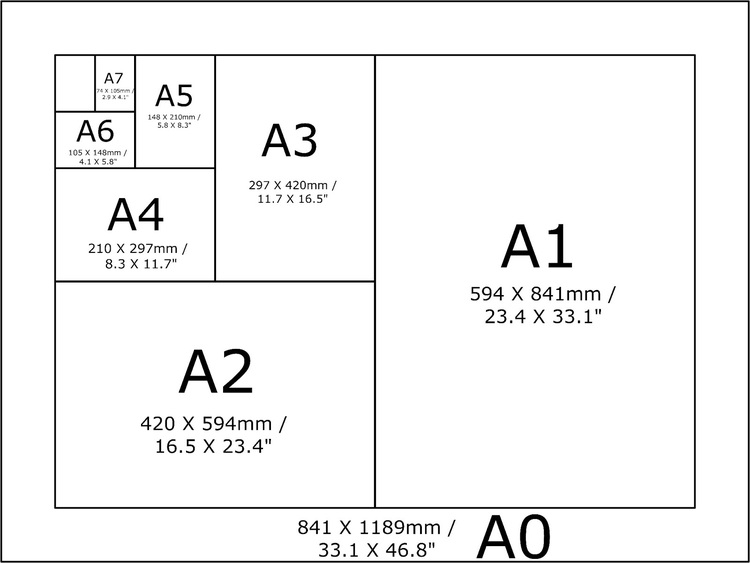ISO 216 specifies international standard (ISO) paper sizes. All ISO paper sizes (except DL) have the same aspect ratio , $1:\sqrt 2$ . This ratio has the unique property that when cut or folded in half width-wise, the halves also have the same aspect ratio.

Suppose I define a paper series $R$ with the same aspect ratio, although this is rounded to the nearest millimetre. If the starting element $R0$ has an area of $(150 \times 212) \text{ mm}^2$ , what will be the area of $R4$ in $\text{mm}^2$ ?

The answer is 1961.

1 solution

Chew-Seong Cheong
Oct 19, 2018

Let the dimensions of $Rn = a_n \times b_n$ , where $n$ is a non-negative integer and $a_n : b_n = 1 : \sqrt 2$ . We note that $a_{n+1} = \dfrac {b_n}2$ and $b_{n+1} = a_n$ . Then we have the following table. Note that $a_4 = \dfrac {b_3}2 = 37.5$ , which is round down to $37$ because is cut.

$\begin{array} {lrcrcr} R0: & 150 & \times & 212 & = & 31800 \\ R1: & 106 & \times & 150 & = & 15900 \\ R2: & 75 & \times & 106 & = & 7950 \\ R3: & 53 & \times & 75 & = & 3975 \\ R4: & 37 & \times & 53 & = & \boxed{1961} \end{array}$

New Paper Size R4

The answer is 1961.

1 solution

0 pending reports