New Year Problem (1)

We can prove by induction that for any positive $n$ , the following is true: $1^3+2^3+3^3+\dots+n^3 = (1+2+3+\dots+n)^2=\Bigg(\frac{n(n+1)}{2}\Bigg)^2$

The following identity is true for all $n \in \N\newline 1^3 + 2^3 + 3^3 + \cdots +n^3 = (1 + 2 + 3 + \cdots + n)^2 = \Large\Bigg(\frac{n(n+1)}{2}\Bigg)^2\newline$ This can be proved by mathematical induction but here I have a geometrical understanding to conclude this.

Here consider two terms : CUBOID $(S)$ and CUBE $(C)$ . CUBOID is always of thickness 1 unit and other dimensions as given in description with term $S$ . For example, $S(a,b)$ means volume of cuboid of dimensions $a, b, 1$ , and $S(a)$ means volume of cuboid of dimensions $a, a, 1$ . Similarly CUBE is defined by dimension along with term $C$ . For example, $C(a)$ means volume of cube of edge length $a$ .

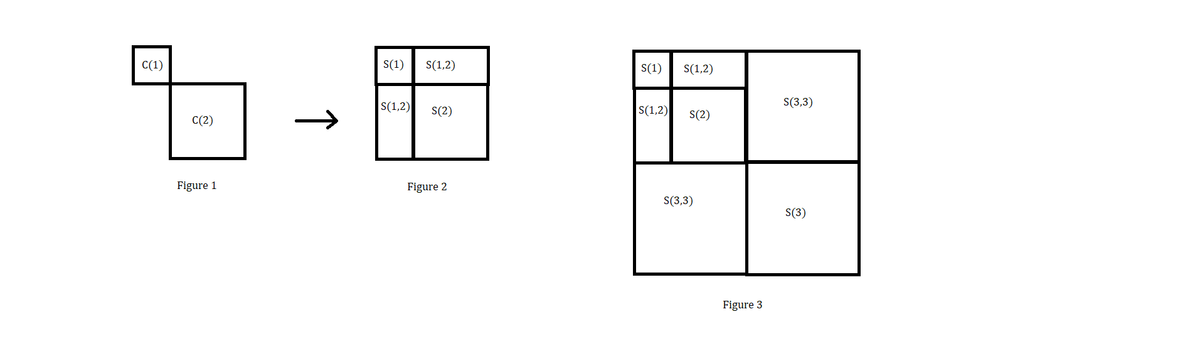
Figure 1 shows 2 cubes of edge 1 and 2 (thickness is not shown) . $\newline C(1) = S(1)\newline$ Cube of side length 2 can be broken into 1 cuboid $S(2)$ and 2 cuboid $S(1,2)\newline C(2) = S(2) + 2S(1,2)\newline \Rightarrow C(1) + C(2) = S(1) + S(2) + 2S(1,2) = S(1+2)$ (see figure 2) $\newline \Rightarrow 1^3 + 2^3 = (1+2)^2$

Similarly, $\large C(n) = n^3 = n^2(n-1) + n^2\newline \hspace{70pt} = 2\Bigg(\frac{(n-1)n}{2}\Bigg)n + S(n)\newline \hspace{70pt} = \large2S\Bigg(\frac{(n-1)n}{2}, n\Bigg) + S(n)\hspace{40pt} \cdots\text{ Eq. 1 }\newline$ . Putting $n = 3$ we get $\newline C(3) = 2S(3,3) + S(3)\newline$ . From figure 3, we see that $C(1) + C(2)+ C(3) = S(1+2) + 2S(3,3) + S(3) = S(1+2+3)\newline \Rightarrow 1^3 + 2^3 + 3^3 = (1+2+3)^2\newline$ Similarly continuing from figure 3 by putting $n = 4$ in Eq. 1 and placing $S(4)\text{ on the corner of figure 3 and } S(6,4)\text{ along the sides of square as shown in figure 4 we conclude that }\newline 1^3 + 2^3 + 3^3 + 4^3 = (1+2+3+4)^2$

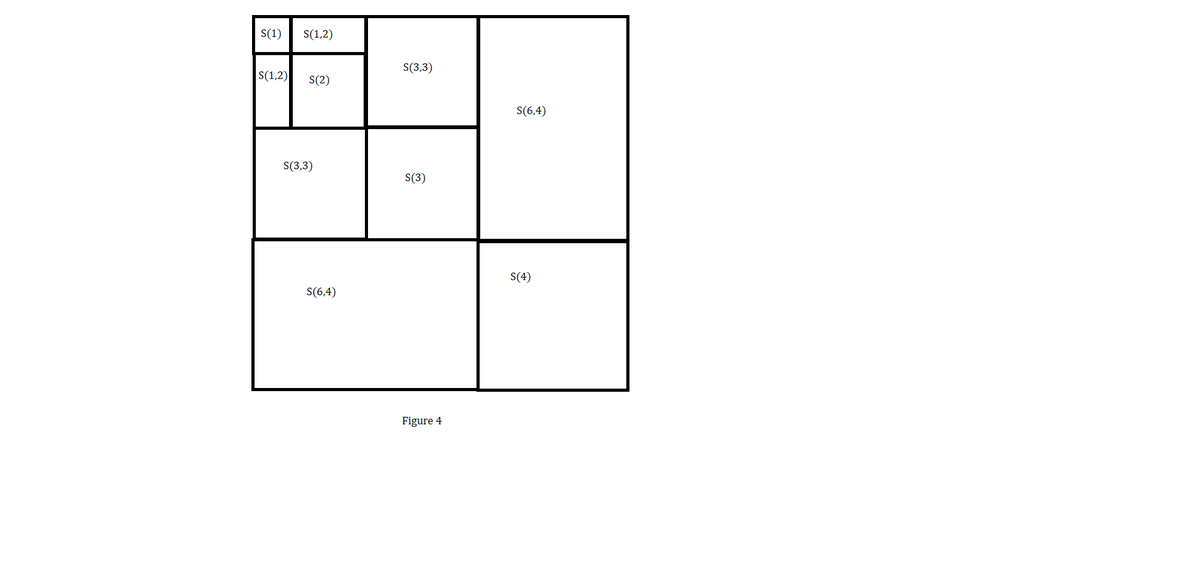
This can be continued further. So whenever it is true that $1^3 + 2^3 + 3^3 + \cdots +n^3 = (1 + 2 + 3 + \cdots + n)^2$ for $n = k-1$ . Then by putting $n= k \text{ in Eq. 1 and placing the cuboids as described we can conclude that the equation is true for } n = k. \text{ Hence it is true for all } n \in \N$