New Year's Countdown Day 27: Triangle Tricks
In △ A B C , ∠ B = 9 0 ∘ and A C = 2 B C . A point P is located in the interior of △ A B C such that P A = 2 7 P B and ∠ A P B = 1 2 0 ∘ . The value of ( P B P C ) 2 can be expressed in the form q p , where p and q are relatively prime positive integers. Find the value of p + q .
This problem is part of the set New Year's Countdown 2017 .
The answer is 682.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I missed because I pressed the wrong button and a wrong sign in Cos Rule.
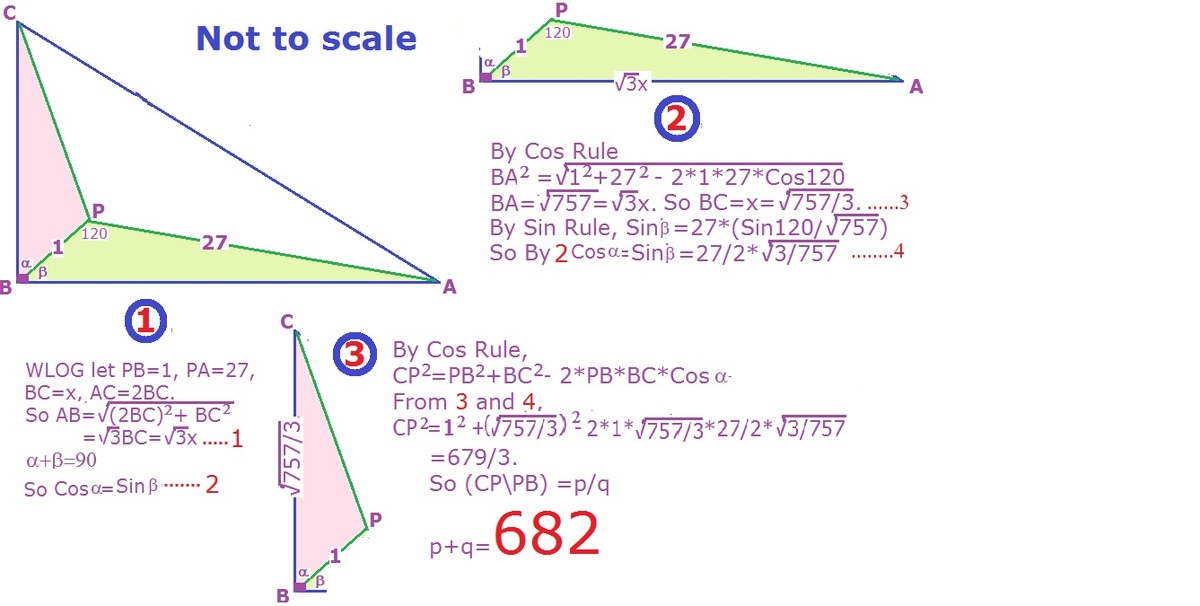
O R I n Δ A B C f r o m t h e g i v e n d a t a ; − B A 2 = ( 2 B C ) 2 − ( B C ) 2 = 3 B C 2 . ∴ B C 2 = 3 B A 2 . . . . . . . . . . . . . . . . . . ( 1 ) S i n P B A = C o s P B C , . . . . . . . . . . . . . . . . . . . . . . . . . ( 2 ) S i n c e ∠ P B A + ∠ P B C = 9 0 o . I n Δ P B A : − S i n c e w e a r e i n t e r e s t e d i n r a t i o s a n d g i v e n d a t a d o e s n o t g i v e a n y l e n g t h s W L O G l e t P B = 1 , a n d P A = 2 7 . U s i n g C o s R u l e B A 2 = P B 2 + P A 2 − 2 ∗ P B ∗ P A ∗ C o s P B A = 1 2 + 2 7 2 + 2 ∗ 1 ∗ 2 7 ∗ 2 1 = 7 5 7 . . . . . . . . . . . . . . . . ( 3 ) F r o m ( 1 ) B C = 3 7 5 7 . . . . . . . . . . . . . . . . ( 4 ) U s i n g S i n R u l e S i n P B A = 2 7 ∗ B A S i n 1 2 0 = 2 7 ∗ 7 5 7 2 3 = 2 2 7 ∗ 7 5 7 3 . . . . . . . . . . . . . . . ( 5 ) U s i n g C o s R u l e i n Δ C B P , F r o m ( 1 ) , C P 2 = P B 2 + B A 2 − 2 ∗ P B ∗ B A ∗ C o s C B P . F r o m ( 2 ) , ( 4 ) , ( 5 ) , . . . . = 1 2 + ( 3 7 5 7 ) − 2 ∗ 1 ∗ 3 7 5 7 ∗ 7 5 7 3 ∗ 2 2 7 . = 1 + 3 7 5 7 − 2 7 = 3 6 7 9 . p + q = 6 7 9 + 3 = 6 8 2 .
Let P B = x , so that P A = 2 7 x . Using the Law of Cosines on △ A P B , we have
A B 2 = P A 2 + P B 2 − 2 ( P A ) ( P B ) cos ∠ A P B = x 2 + ( 2 7 x ) 2 − 2 x ( 2 7 x ) cos 1 2 0 ∘ = x 2 + 7 2 9 2 + 2 7 x 2 = 7 5 7 x 2 .
Thus, A B = x 7 5 7 .
Let O be the midpoint of A B . From the given information about △ A B C , we deduce that it is a 30-60-90 right triangle, so O is also the circumcenter of △ A B C . This gives us
B C = C O = O A = O B = 3 A B = x 3 7 5 7 .
Since ∠ B O A = ∠ B P A = 1 2 0 ∘ , quadrilateral B P O A is a cyclic quadrilateral. By Ptolemy's theorem,
B P ⋅ O A + B A ⋅ O P x ( x 3 7 5 7 ) + x 7 5 7 ⋅ O P 3 x + O P O P = B O ⋅ A P = ( x 3 7 5 7 ) ( 2 7 x ) = 3 2 7 x = 3 2 6 x .
Now, we focus on △ B C O . Since B C = C O = O B , △ B C O is equilateral:
We also have ∠ B P O = 1 5 0 ∘ , since it is supplementary to ∠ B A C = 3 0 ∘ . To find the length of P C , we rotate △ B P O clockwise 6 0 ∘ about O to form a new triangle:
Since rotations preserve distances, O P = O P ′ and B P = B ′ P = x . This means △ P O P ′ is isosceles, and ∠ P P ′ O = ∠ P ′ P O . We also have ∠ P O P ′ = 6 0 ∘ , since that is the angle of rotation. Thus,
∠ P P ′ O = ∠ P P ′ O = 2 1 8 0 ∘ − ∠ P O P ′ = 2 1 8 0 ∘ − 6 0 ∘ = 6 0 ∘ ,
and △ P O P ′ is equilateral. This gives us P P ′ = P O = 3 2 6 x .
Since ∠ B ′ P ′ O = ∠ B P O = 1 5 0 ∘ , ∠ B ′ P ′ P = 1 5 0 ∘ − 6 0 ∘ = 9 0 ∘ , meaning △ B ′ P ′ P is a right triangle. By the Pythagorean Theorem,
P C 2 = P P ′ 2 + B ′ P ′ 2 = ( 3 2 6 x ) 2 + x 2 = 3 6 7 6 x 2 + x 2 = 3 6 7 9 x 2 .
Finally, P C = x 3 6 7 9 , so ( P B P C ) 2 = 3 6 7 9 , and p + q = 6 7 9 + 3 = 6 8 2 .