Newton Raphson Works Great, Until It Doesn't - Part 1
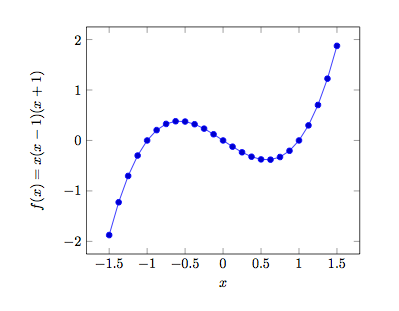 Consider the function given by
f
(
x
)
=
x
(
x
−
1
)
(
x
+
1
)
. If we apply the
Newton Raphson method
with the approximate root
x
0
=
0
.
4
5
, which root would we converge to?
Consider the function given by
f
(
x
)
=
x
(
x
−
1
)
(
x
+
1
)
. If we apply the
Newton Raphson method
with the approximate root
x
0
=
0
.
4
5
, which root would we converge to?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Corrrrrrrrrrrect... :)
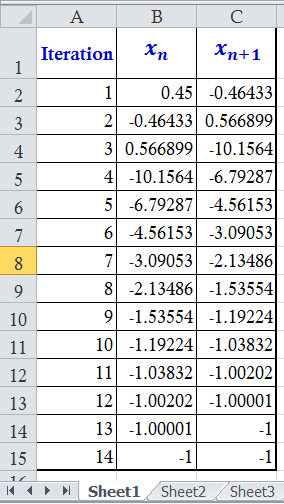
Using Ms. Excel spreadsheet, we can obtain the root will converge to
−
1
for initial value
x
0
=
0
.
4
5
. Take a look the picture below.
 Newton Raphson
Newton’s (or the Newton-Raphson) method is one of the most powerful and well-known
numerical methods for solving a root-finding problem. Newton’s method is an extremely powerful technique because it is rapidly convergent than any other methods. In this case, it takes only
1
4
iterations to yield the root of
f
(
x
)
=
x
(
x
−
1
)
(
x
+
1
)
. Iteration should be stopped if
x
n
=
x
n
+
1
or
∣
x
n
−
x
n
+
1
∣
=
ϵ
, where
ϵ
is the tolerance value and it is chosen as close as possible to
0
for yielding the best accuracy of the root of function.
Newton Raphson
Newton’s (or the Newton-Raphson) method is one of the most powerful and well-known
numerical methods for solving a root-finding problem. Newton’s method is an extremely powerful technique because it is rapidly convergent than any other methods. In this case, it takes only
1
4
iterations to yield the root of
f
(
x
)
=
x
(
x
−
1
)
(
x
+
1
)
. Iteration should be stopped if
x
n
=
x
n
+
1
or
∣
x
n
−
x
n
+
1
∣
=
ϵ
, where
ϵ
is the tolerance value and it is chosen as close as possible to
0
for yielding the best accuracy of the root of function.
# Q . E . D . #
The problem doesn't require any table of iterations. We simply apply Newton's method once. We first find f ′ ( 0 . 4 5 ) :
f ( x ) = x 3 − x ⟹ f ′ ( x ) = 3 x 2 − 1
Plugging in x = 0 . 4 5 gives us f ′ ( 0 . 4 5 ) ≈ − 0 . 3 9 7 5 . Now we need to find the equation of this tangent line and determine it's x-intercept. We know it goes through the point ( 0 . 4 5 , f ( 0 . 4 5 ) ) = ( 0 . 4 5 , − 0 . 3 5 8 8 ) . Using this information we determine the equation of the tangent line and then its x-intercept:
y = − 0 . 3 9 7 5 x − 0 . 1 7 9 9 2 5 ⟹ x i n t ≈ − 0 . 4 5 2 .
Since we know that f ( x ) = 0 at x = 0 , 1 , − 1 , and the first iteration of Newton's method yields a negative x-intercept, then after a sufficient number of iterations, the root will converge to x = − 1 . And we're done.
Note that the argument above is correct because if the root converged to x = 1 , then the first iteration would yield an x-intercept such that 0 . 4 5 < x i n t < 1 . If it was converging to x = 0 then the first iteration would yield an x-intercept such that 0 < x i n t < 0 . 4 5 . However neither of these is true. Therefore we know for a fact that the root converges to x = − 1 by the above logic.
Note: The point of this post is to prove the validity of the logic used in the solution to arrive upon the answer.
just simply like this x+1 = 0 so that x = -1 .. -1 is the answer
Most people would likely have chose the option of 0, because that is the closest root to 0 . 4 5 .
However, if you applied the Newton Rahpson method, you would noticed that the approximated roots swing around some. In particular, if f ′ ( x ) is close to 0, then the next approximate root will be quite far away (see n = 2 below).
Here is the table of values, if you followed the method accordingly:
Hence, with a starting approximation of 0.45, we actually end up with the root of -1!