Newton's Law Of Cooling

Classical Mechanics Level 2

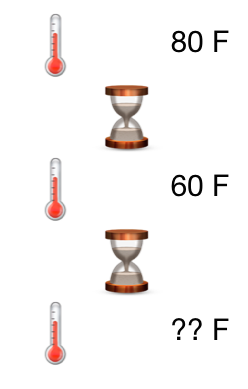
A thermometer reading 8 0 ∘ F 80^\circ F is taken outside.
Five minutes later the thermometer reads 6 0 ∘ F 60^\circ F .
After another 5 minutes it reads 5 0 ∘ F 50^\circ F .

What is the temperature outside ( ( in ∘ F ) ? ^\circ F)?

Assume that this process follows Newton's law of cooling.


The answer is 40.

Rishabh Jain by Rishabh Jain , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Let the initial and final temperatures of the body be ( T 1 T_1 ) and ( T 2 T_2 ), time taken for the temperature to change be t t and temperature of the surroundings be T T .

By Newton's law of cooling we have,

( T 1 − T 2 ) / t = K ( ( T 1 + T 2 ) / 2 − T ) (T1-T2)/t = K((T1+T2)/2 - T) , where K K is a constant.

Substituting the temperatures in of the above two cases, we obtain two equations.

4 = K ( 70 − T ) 4 = K(70-T) and 2 = K ( 55 − T ) 2 = K(55-T) .

Solving both equations we get T = 40 T=40 . Therefore, the temperature of the surrounding is 40 degrees Fahrenheit .

5 Helpful 0 Interesting 0 Brilliant 0 Confused
Vikash Singh
Mar 19, 2016

Just guessed the answer in one go :D

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Newton's Law of Cooling is T(final)=T(ambient)+(T(initial)-T(ambient)*e^(-kt) where k=constant and t= time elapsed

In this case,

60=T(ambient)+(80-T(ambient)*e^(-5k) ( equation 1)

50=T(ambient)+(80-T(ambient)*e^(-10k) ( equation2)

k= log2/5 and T ambient is 40

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...