Mechanics - 2

Classical Mechanics Level 2

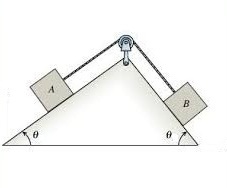
What are the acceleration of the blocks and tension in the string respectively?

Assumptions and Details:

  • Mass of block A A , m A = 3 kg m_A = \text{3 kg}
  • Mass of block B B , m B = 5 kg m_B = \text{5 kg}
  • Angle of incline, θ = 3 0 ∘ \theta = 30^\circ
  • Acceleration due to gravity, g = 10 m/s 2 g = \text{10 m/s}^2
  • The string is massless and inextensible.
  • The pulley is massless and there is no friction in the pulley and with the string.

Try my World of Physics to solve many problems like this one.

1.5 m/s 2 , 15.75 N \text{1.5 m/s}^2 \text{, 15.75 N} 1.75 m/s 2 , 12.75 N \text{1.75 m/s}^2 \text{, 12.75 N} 1.25 m/s 2 , 18.75 N \text{1.25 m/s}^2 \text{, 18.75 N} 1 m/s 2 , 18.75 N \text{1 m/s}^2 \text{, 18.75 N}

Ram Mohith by Ram Mohith , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Chew-Seong Cheong
Jan 25, 2019

By Newton's second law , we have:

  • The acceleration of the blocks m B g sin ⁡ θ − m A g sin ⁡ θ = ( m A + m B ) a m_Bg \sin \theta - m_Ag \sin \theta = (m_A + m_B) a ⟹ a = m B − m A m A + m B g sin ⁡ θ \implies a = \dfrac {m_B-m_A}{m_A+m_B}g\sin \theta = 5 − 3 5 + 3 ( 10 ) ( 0.5 ) = 1.25 m/s 2 =\dfrac {5-3}{5+3}(10)(0.5) = \text{1.25 m/s}^2 .
  • The tension in the string T = m B g sin ⁡ θ − m B a T = m_Bg\sin \theta - m_Ba = 5 ( 10 × 0.5 − 1.25 ) = 18.75 N =5(10\times 0.5-1.25) = \text{18.75 N} .

Therefore, the answer is 1.25 m/s 2 , 18.75 N \boxed{\text{1.25 m/s}^2 \text{, 18.75 N}} .

0 Helpful 0 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...