Mechanics - 3
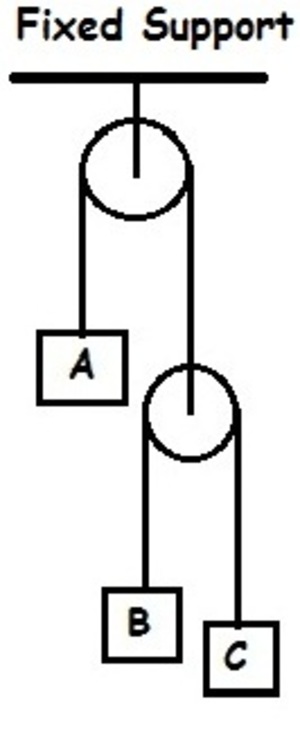
Given that:
- the velocity of A with respect to C , v A C = 300 m/s ↑ (note the direction of the velocity)
- the velocity of B with respect to A , v B A = 200 m/s ↓ .
Find the absolute velocity of A , v A .
Assumptions:
- The strings are massless and inextensible.
- The pulleys are massless and there is no friction in the pulley and between the string and pulley.
Try my World of Physics to solve many problems like this one.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let us denote ↑ direction as + and ↓ direction as − . Then we have { v A C = v A − v C = 3 0 0 v B A = v B − v A = − 2 0 0 . . . ( 1 ) . . . ( 2 )
From ( 1 ) + ( 2 ) : v B − v C = v B C = 1 0 0 . Since, with respect to the right pulley P , v B P = − v C P , ⟹ − 2 v C P = 1 0 0 or v C P = − 5 0 . We know that the velocity of the right pulley, v P = − v A . Then we have:
v A C v A − v C v A − ( v P + v C P ) v A − ( − v A − 5 0 ) 2 v A ⟹ v A = 3 0 0 = 3 0 0 = 3 0 0 = 3 0 0 = 3 0 0 − 5 0 = 125 m/s ↑
Typos in equation (2)
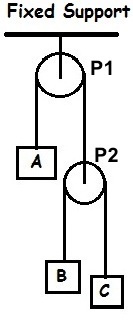 Let us refer all velocities to
A
.
V
B
A
=
2
0
0
m/s
↓
.
Let us refer all velocities to
A
.
V
B
A
=
2
0
0
m/s
↓
.
Being v A C = 3 0 0 m/s ↑ , the veloctity of C referred to A is v C A = 3 0 0 m/s ↓ , and v A A = 0 , of course.
The velocity of P 2 referred to A must be v P 2 A = 2 v B A + v C A = 2 3 0 0 m/s ↓ + 2 0 0 m/s ↓ = 2 5 0 m/s ↓ , since B approaches the pulley at the same speed C receeds from it.
Likewise, the velocity of P 1 referred to A must be v P 1 A = 2 v A A + v P 2 A = 2 0 + 2 5 0 m/s ↓ = 1 2 5 m/s ↓ .
Since we know P 1 must be zero in earth's reference frame, we must add 1 2 5 m/s ↑ to all velocities:
v C = 1 7 5 m/s ↓ , v B = 7 5 m/s ↓ and v A = 1 2 5 m/s ↑
Based on the given information, v A − v C = v A C = 3 0 0 ⟹ v C = v A − 3 0 0 v B − v A = v B A = − 2 0 0 ⟹ v B = v A − 2 0 0
Now call the lower pulley P and note that v P = − v A v B − v P = v B P = − v C P = v P C = v P − v C so that ( v A − 2 0 0 ) + v A = − v A − ( v A − 3 0 0 ) ⟹ v A = 4 5 0 0 = 1 2 5 where the direction is ↑ because we have oriented all positive measurements to be up.