Newton's Logical Mechanics
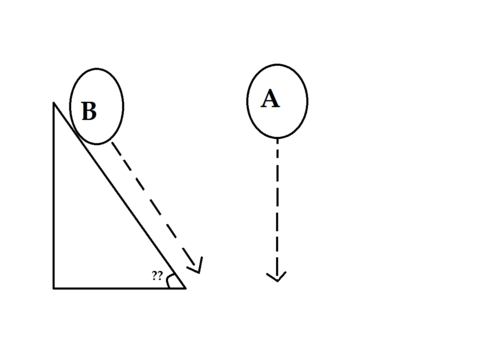 Two balls
, and
are kept at a certain height from where ball
is dropped freely and Ball
is rolled through a wedge with coefficient of friction
. Given that
,
are the final velocities of balls
, and
respectively with a relation that.
Find the angle of inclination of the wedge in degrees, rounded to the nearest integer
Two balls
, and
are kept at a certain height from where ball
is dropped freely and Ball
is rolled through a wedge with coefficient of friction
. Given that
,
are the final velocities of balls
, and
respectively with a relation that.
Find the angle of inclination of the wedge in degrees, rounded to the nearest integer
Note:
-
The balls are identical
-
Ball B is not Rolling
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the balls be kept at height h from the ground.
Now we can find the velocity of ball A by using equations of motion. In this case acceleration of ball A is g
So V A 2 = 2 g h
Now acceleration of ball B is g ( s i n θ − μ c o s θ ) (we can get this by making free body diagrams and then using Newton's 2nd law)
So V B 2 = 2 g ( s i n θ − μ c o s θ ) s i n θ h
But
V A = 2 2 V B
So 2 g h = 2 2 2 g ( s i n θ − μ c o s θ ) s i n θ h
On squaring both sides we get
1 = 8 ( 1 − μ c o t θ )
or c o t θ = 3 4
So θ = a r c c o t ( 3 4 ) ≈ 3 7 :)