Newton's Sum is very popular
⎩ ⎪ ⎨ ⎪ ⎧ x x 2 x 3 + + + y y 2 y 3 + + + z z 2 z 3 = = = 1 3 7
If x , y and z satisfy the values of the system of equations above, find the value of x 5 + y 5 + z 5 .
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
That's one of the best handwriting I've ever seen!!!
WOw! Very nice fonts! +1
I actually don't know about newtons identity. enlighten me please?
So, what are x, y and z then?
Log in to reply
Doesn't matter. We were asked to find the value of x 5 + y 5 + z 5 only.
For what it's worth: The unordered solution is ( x , y , z ) ≈ ( − 0 . 4 1 9 6 4 3 + 0 . 6 0 6 2 9 1 i , − 0 . 4 1 9 6 4 3 − 0 . 6 0 6 2 9 1 i , 1 . 8 3 9 2 9 ) .
Please teach me a little about Newton's identities. Actually I have not been taught it yet. I just need the basic idea of how,where and when they are to be used. Thanks in advance.
Log in to reply
Read the relevant wiki.You can search for Newton's Identities in the search bar to find the wiki.
Although I did it using newton Girard identity but I'm pretty sure that you can even do it using other ways too. Probably using brute calculations and binomial theorem or like anshu jha's method
Nice approach to solve the question... anyway it's lot easier than the cliched "Newton sums".
...by the way how did you find xyz without using newton sums... i mean which identity did u use??
Log in to reply
x^3 + y^3 + z^3 - 3xyz = (x+y+z)(x^2 + y^2 + z^2 - xy - xz - yz)
I did this way but I think Sir Newton's identities would make it much simpler. 😀😀
The pattern 1,3,7 increases the difference between consecutive terms by 2. The terms then become 1,3,7,13,21. I know this isn't really a solution buts it how I "solved" it .
Nice observation but patterns can "fool" you. For example, you could suppose that the difference between consecutive termes are consecutive powers of 2. That would lead you to think that the solution is 31.
I do not know if this counts as a pure mathematical\algebraic solution.
Given the system:- x + y + z = 1
x^2 + y^2 + z^2 = 3
x^3 + y^3 + z^3 = 7
If we observe closely there is a pattern here, which could be generalised into a equality given by:-
x^n + y^n + z^n = n^2 - n + 1
This holds true for all the 3 given equalities.
eg. x + y +z = x^1 + y^1 + z^1 (here n=1) = 1^2 - 1 + 1 = 1
eg. x^2 + y^2 + z^2 (here n=2) = 2^2 - 2 + 1 = 4 - 2 + 1 = 3
eg. x^3 + y^3 + z^3 (here n=3) = 3^2 - 3 + 1 = 9 - 3 + 1 = 7
Therefore,
x^5 + y^5 + z^5 = 5^2 - 5 + 1 = 25 - 5 + 1 = 21
Thanks for sharing your approach.
I would say that this is a coincidence that you found a formula for n = 1 , 2 , 3 and it holds true for n = 5 also. According to your formula, when n = 4 , you get 4 2 − 4 + 1 = 1 3 . However, the correct value of x 4 + y 4 + z 4 is 1 1 . Please have a look at Jessica Wang's solution to see the correct method.
Uhm. I get the answer by adding multiples of 2 on the answer. 1+2=3; 3+4=7; 7+6=13; 13+8=21. HAHAHA
Let $\ p=a+b+c$, $\ q=ab+bc+ca$ and $\ r=abc$, we have some useful identities between $\ p, q, r$ and $\ a^n+b^n+c^n$
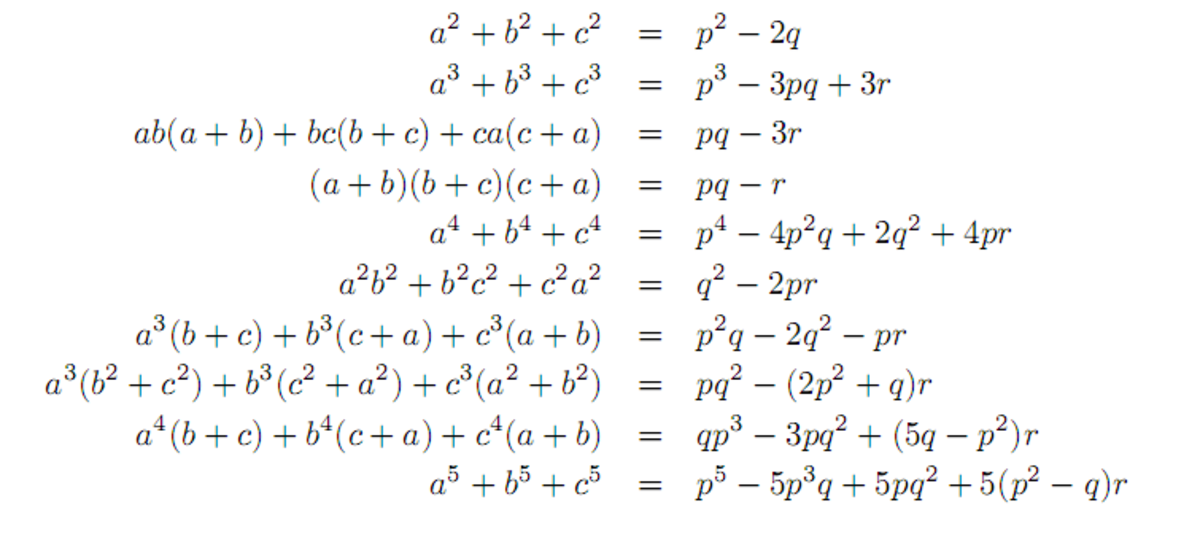
p/s: this picture was cut from a book about Inequality (PQR technique) which was written by V.Q.B.Can
don't need any fancy math skills for this (yes including solving it simultaneously!). All you need to notice is that there is a sequence: EQU 1 --> EQU 2 you add 2 to the solution; EQU 2 --> EQU 3 you add 4; EQU 3 --> EQU 4 you add 6; EQU 4 --> EQU 5 you add 8. So in the end you get 1+2=3; 3+4=7; 7+6=13; 13+8=21. QED, the answer is x^5 +y^5 +z^5=21.
Except if you actually solve the equation, x^4 + y^4 + z^4 = 11.

Relevant wiki: Newton's Identities